微分：解码宇宙的变化之语

引言：微分，这个由牛顿和莱布尼茨奠基的数学概念，不仅是描述自然界瞬时变化的精确工具，更是洞察宇宙本质的哲学镜头。它揭示了变化与恒常、无限与有限之间的深刻联系，为我们理解世界提供了全新的视角。

瞬间的永恒：导数的哲学意义

在宇宙的永恒流变中，导数概念捕捉到了瞬间的本质。当我们将时间间隔无限缩小，趋近于零时，差商的极限揭示了变化的本质：

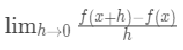
这个看似简单的公式蕴含着深刻的哲学意义。它告诉我们，真理往往存在于极限状态，而非有限的观察中。这启发我们思考：在生命和社会的变迁中，什么是真正的本质？我们是否也能通过观察"瞬时变化"来洞察事物的本质？

导数不仅是数学工具，更是一种思维方式。它教会我们在变化中寻找规律，在动态中把握静态。从个人成长到社会进步，或许我们都需要学会计算自己的"人生导数"，找到最优的发展方向。

无限与有限的交响：极限思想的启示

极限思想是微分的核心，它巧妙地将无限与有限联系起来。当我们考虑函数f(x)在x → a时的导数：

我们实际上是在探索有限世界中的无限可能。这种思维方式对于理解宇宙的本质至关重要。从宏观的宇宙膨胀到微观的量子涨落，极限思想都提供了独特的洞察。

在哲学层面，极限思想启发我们思考：人类的认知是否也存在某种"极限"？我们是否能通过不断接近这个极限，来逐步揭示真理的本质？这种思维方式鼓励我们在探索未知时保持开放和谦逊的态度。

变化的普适语言：导数在多领域的应用

导数作为描述变化率的普适语言，其应用远超出数学领域。在物理学中，它描述了速度和加速度；在经济学中，它解释了边际效应；在工程学中，它优化了设计过程。这种跨学科的普适性揭示了一个深刻的真理：尽管表象各异，变化的本质可能遵循着相同的规律。

这启发我们思考：是否存在一种统一的"变化语言"，可以描述宇宙中所有的变化过程？从个体的成长到社会的进步，从生命的演化到宇宙的扩张，我们是否能用同一种方式来理解这些看似不同的变化？

优化与平衡：导数的哲学启示

导数在优化问题中的应用，如求函数的极值点：

f′(x) = 0

揭示了一个深刻的道理：最优状态往往存在于变化的临界点。这一原理不仅适用于数学函数，在生态系统、经济模型、甚至个人生活中都有深远的启示。

这启发我们思考：在追求进步的过程中，如何找到增长与平衡的最佳点？在个人发展中，如何在不同目标之间寻找最优的平衡？导数思维教导我们，真正的智慧不在于盲目追求极端，而在于找到那个微妙的平衡点。

连续性与突变：导数的存在性探讨

导数的存在条件揭示了连续性与可微性之间的微妙关系。并非所有连续函数都是可微的，这一事实启发我们思考：在自然界和社会中，平滑的变化和突然的跃迁是如何共存的？从量子跃迁到社会革命，突变现象似乎暗示着世界的本质可能并非总是连续可微的。

这种思考引导我们重新审视变化的本质：是否所有的变化都可以用微分来描述？在面对复杂系统时，我们是否需要新的数学工具和思维方式来理解那些不连续、不可微的变化？

结语：微分不仅是一种数学工具，更是一种理解世界的哲学。它教会我们在变化中寻找不变，在有限中探索无限，在复杂中发现简单。通过微分的镜头，我们得以一窥宇宙的运行法则和生命的本质。在这个日益复杂的世界中，微分思维为我们提供了一种洞察本质、把握全局的方法，引导我们在科学、哲学和生活的道路上不断前行。让我们携带这种思维，继续探索宇宙的奥秘，解读生命的密码。

关键词：瞬时变化、极限思想、普适语言、优化平衡、连续与突变、哲学思维、宇宙洞察、生命本质