梯度，作为一个重要的数学概念，在多个领域，特别是机器学习领域，扮演着至关重要的角色。本文将从梯度的基本概念出发，探讨其在机器学习中的应用，重点介绍梯度下降算法及其在实际问题中的具体应用案例。

梯度是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值。换句话说，函数在该点处沿着梯度的方向变化最快，变化率最大（梯度的模即为该最大方向导数的值）。在多元函数中，梯度是由各参数的偏导数组成的向量，它指明了函数值增长最快的方向。

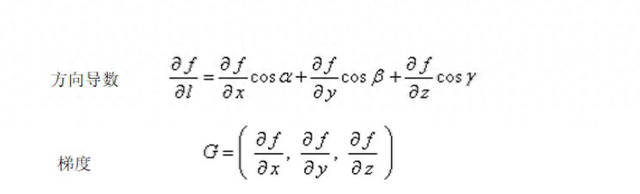
在三维空间中，如果函数f(x, y, z)在某点P具有一阶连续偏导数，那么向量∇f(P)就是函数在点P的梯度，其中∇是向量微分算子或Nabla算子。梯度不仅指明了函数值增长最快的方向，其模还反映了函数曲面在该点变化的剧烈程度。

在机器学习领域，梯度主要用于优化算法中，特别是用于寻找损失函数的最小值。损失函数是衡量模型预测值与真实值之间差异的函数，优化损失函数的过程就是训练模型的过程。梯度下降是其中一种非常常见且有效的优化算法。

梯度下降算法的基本思想是从一个初始点开始，沿着梯度的反方向（即损失函数下降最快的方向）逐步更新模型参数，以期达到损失函数的最小值。这一过程类似于从山顶沿着最陡峭的路径下山，直到到达山脚（或局部最低点）。

具体实现时，通常使用随机梯度下降（SGD）或其变种，如Adam、RMSprop等。这些算法通过迭代更新模型参数，每次迭代都使用一部分数据（或全部数据）来计算梯度，并根据梯度调整参数。

线性回归是机器学习中最基本的应用之一，其目标是通过一条直线（或曲线）拟合数据点，使得预测值与真实值之间的误差最小。在这个过程中，梯度下降算法被用于优化损失函数，通常是均方误差（MSE）。

设数据集为{(x_1, y_1), (x_2, y_2), ..., (x_n, y_n)}，线性回归模型为y = wx + b。我们希望找到最佳的w和b，使得损失函数J(w, b)最小。J(w, b)通常定义为所有预测值与真实值之差的平方和的平均值。

梯度下降算法会计算损失函数对w和b的偏导数（即梯度），然后沿着梯度的反方向更新w和b的值，直到损失函数收敛到最小值或达到预定的迭代次数。

梯度提升（Gradient Boosting）是另一种利用梯度进行优化的算法，但与梯度下降不同，梯度提升是通过构建多个弱学习器（如决策树）来逐步逼近最优解。每个弱学习器都尝试拟合前一个学习器的残差（或负梯度），通过累加这些弱学习器的预测结果，最终得到一个强学习器。

梯度提升算法在回归、分类和排序等多种机器学习任务中都有广泛应用，其强大的泛化能力和对异常值的鲁棒性使其成为许多复杂问题的首选解决方案。

梯度作为函数变化最快的方向，在机器学习中具有极其重要的应用价值。通过梯度下降和梯度提升等优化算法，我们可以有效地找到损失函数的最小值，从而训练出性能优异的机器学习模型。随着数据量的增加和计算能力的提升，梯度类优化算法在机器学习领域的应用前景将更加广阔。