班上同学纷纷表示,题目太难了、完全没有头绪!结果可想而知:全军覆没,班上50多人,一个做对的都没有,学霸也不例外!这是一道小学五年级数学竞赛题:长方形长宽均未知,咋求其面积?如图一,

图一
E、F分别为长方形ABCD边BC和CD的中点,过点C作一直线GF,与AE和AF的延长线分别相交于点G和H,三角形CEG和CFH的面积均为12,求长方形ABCD的面积。
难点:未告知①点C在GH所处位置?②EF与GH的关系?连接AC和EF,如图二

图二
C为GH的中点!由E、F均为中点可知,S△ACE=S△ACF=1/4S长方形ABCD。又S△CEG=S△CFH=12,故S△ACG=S△ACH。注意到△ACG与△ACH等高,因此C为GH的中点。
EF⫽CG!由C为GH中点以及S△CEG=S△CFH=12,可知△CEG与△CFH等高,故EF⫽CG!
解析一:不超纲,适合小学生①延长AG与DB相交于点M,连接HM,则CM=CD,AE=EM,如图三
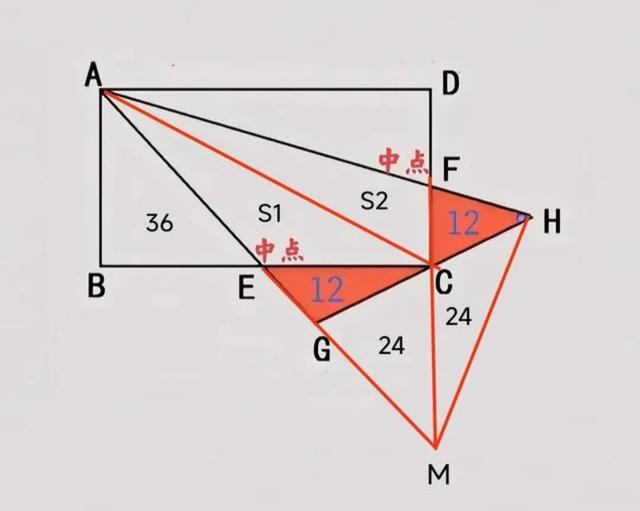
图三
②由CM=2CF可知,S△CHM=2S△CFH=24。由此前结论可知C为中点,故S△CGM=S△CHM=24。
③等底等高三角形面积相等,故S△ABE=S△CEM=36,从而S长方形ABCD=4S△ABE=144。
解析二:超纲,适合中学生!①连接BD,分别与AG和AH相交于点O和点P,如图四

图四
②显然,EF⫽BD。由此前结论EF⫽GH,可知GH⫽BD。又F为CD中点,故S△DFP=S△CFH=12。
③由F为CF中点可知AP=2PF,故S△ADF=36,从而S长方形ABCD=36×4=144。
解析三:不超纲,适合小学生!①过点G作AD的垂线GM,连接DH、DG和BG,如图五

图五
②由同底等高三角形面积相等,可知S△ABG=S△ABM,S△CDG=S△CDM。故S△ABG+S△CDG=S△ABM+S△CDM=1/2S长方形ABCD。
③由E、F为中点以及等底等高三角形面积相等,可知S△BEG=S△CEG=12,S△DFH=S△CFH=12。故S△BCG=24,S△CDH=24。
④由前述结论C为GH中点,以及等底等高三角形面积相等,可知S△CDG=S△CDH=24。
⑤由E为BC中点,S长方形ABCD=4S△ABE。
⑥由②-⑤可得,S△ABE+S△BEG+S△CDG=2S△ABE也即S△ABE=12+24=36,故S长方形ABCD=144。
—————————————————
友友们有啥想法或思路,欢迎留言分享!

吴侯
∵E、F皆为中点,∴S△ACE=S△ACF,∴S△ACG=S△ACH,∴CG=CH,连接DH可知S△DCH=24,角ECG+角FCH=90度,将△DCH绕C点旋转180度,得△MCG且MGF三点共线,角ECM=90度,CM=CD,设AB=2y,BC=2x,∴CM=2y,∴S△ECM=36=xy,∴S长方形=4xy=144