《人工智能 从小白到大神》读书笔记
第4章 搭建人工神经网络
在这本书的4.1.2感知器一节,作者带我们用感知器实现了and函数。通过感知器本身在有关维度的“触角”(神经元的树突)收集到各维度的输入信息X=(x1,...,xn)。各维度对应的感知权重W=(w1,...,wn)。首先,不管激活函数是否存在,我们都需要把各维度传来的信号整合到输出所在的维度,然后传递给下一个逻辑判断的感知器(想想一下神经元)。
这也意味着,同一个感知器(神经元)的输入数据和输出数据的类型必然相同。在逻辑判断的感知器里,输入数据类型为布尔型(只有0和1两种情况),因此,输出数据必然也是布尔类型,也即输出结果只有0和1两种数据。这个世界最基础的信号可以说是光电,所以信号的叠加,可以理解为光电信号在不同透明度膜过滤下的叠加,不管是多么微弱的光,它们也是光,除非遇到了透明度wi=0(不透明)的膜。
叠加公式:w1x1+...+wnxn
不过,在这之前,为了求取x1 and x2的值,需要把曾经熟悉的表格转换一下形式:

图1 曾经熟悉的表格

图2 转换后的表格
x1,x2的取值范围用python集合表示,均为{0,1}。那么与x1和x2对应的权重应该是多少?
其实,最简单的权重分配是等概率模型中的概率分配。这里的样本空间为{0,1},其中样本点为0或者1的可能性相同,取其中一个样本点的概率为P=1/2=0.5。2为有限样本空间内样本点的个数。也就是说,我们可以设置权重w1=w2=0.5。
那么,信号叠加的求值公式为:y=w1*x1 + w2*x2,对应图2中,每行x1与x2的取值,我们尝试着计算求值公式的结果值。
x1=0,x2=0,y=0.5*0+0.5*0=0
x1=0,x2=1,y=0.5*0+0.5*1=0.5
x1=1,x2=0,y=0.5*1+0.5*0=0.5
x1=1,x2=1,y=0.5*1+0.5*1=1
有见过x1 and x2 = 0.5的么,今天你就见到了:D。显然仅靠叠加公式计算结果是不够的。
由于需要把结果转换到同一类型的样本空间内,这才有了激活函数一说,现在得想办法将{0,0.5,1}这个样本空间,转换到{0,1}空间。书中的选择是阶跃函数(Sgn)——符号函数,大于时返回1,小于等于0时,返回值为0。
让我们用python代码编写一个Sgn函数:
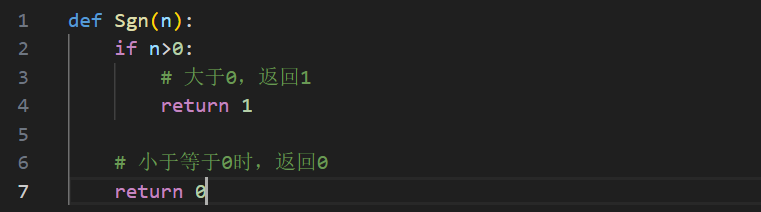
图3 Sgn函数
于是Sgn(0)=0,Sgn(0.5)=1,Sgn(1)=1。也就是说,除了x1=x2=0时,最终转换的结果为0,其余均为1。
大脑经过一阵子的乱序处理后,发现这是or运算的结果,并不是and运算的结果!!!还不错,至少有一半结果是对的,更何况还探索出了or预算的实现:D。豁然发现自我安慰的能力是无与伦比的……
改变从Sgn(0.5)开始,求and结果,必须使得Sgn(0.5)=0。python的round函数倒是满足这个需求,round(0.5)=0,而且round(0)=0,round(1)=1,并不影响其他结果。让我们一起呐喊:在一起,在一起,在一起,……。于是有了Sgn=round。

图4 将Sgn函数替换为python的round函数
图2表格的输入、输出结果完全对上了。
对于这个感知器而言,我们前面的激活函数,其实可以说是感知器本身的喜好。既然有喜好,就意味着命运的天平根据喜好选定不同的支点,而造成的结果绝大多数时候会向天平一端倾斜。但我们换激活函数的情况基本不会发生,为什么不会发生???这是因为一个神经元的激活函数从该神经元诞生的那一刻起,就是确定的。
现在回到最初的Sgn函数(符号函数)。毕竟不好改变Sgn函数,那么试试改变自身的喜好。不妨比较一下最初的Sgn函数和python的round函数计算的结果。
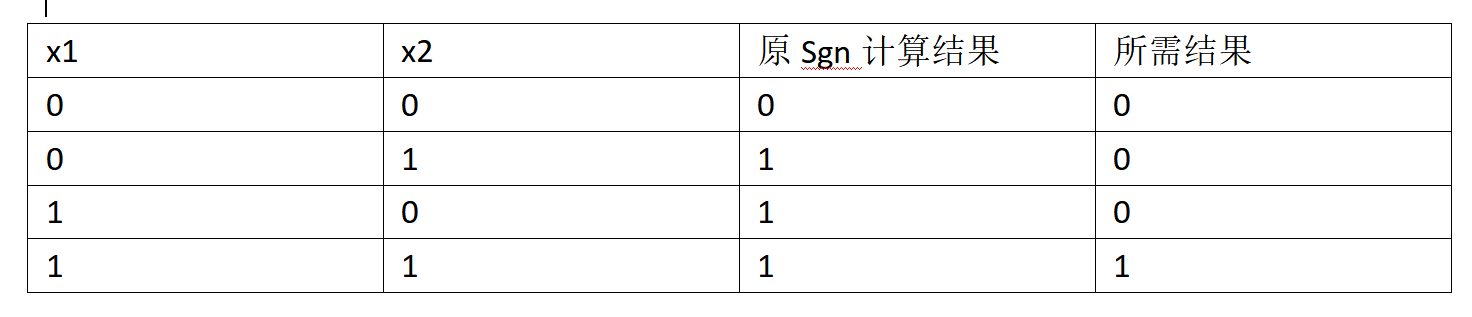
图5 原Sgn函数与所需结果的比较
再退回叠加公式的情形,要得到所需结果,叠加公式最好改成这样:
x1=0,x2=0时 0.5*0+0.5*0+0=0,Sgn函数计算结果为0
x1=0,x2=1时 0.5*0+0.5*1+(-0.5)=0.5+(-0.5)=0,Sgn函数计算结果为0
x1=1,x2=0时 0.5*1+0.5*0+(-0.5)=0.5+(-0.5)=0,Sgn函数计算结果为0
x1=1,x2=1时 0.5*1+0.5*1+0=1,Sgn函数计算结果为1
或者说w1*x1+w2*x2在加上一个数据,比如说是b,使得w1*x1+w2*x2+b除了x1=x2=1的情况外,计算结果小于等于0即可。
为了列方程方便,我们令b=w0*x0,其中w0=b,x0=1(x0为啥为1呢?只要这个神经元“活着”,x0就应该为1),现在调整一下公式:
w0*x0+w1*x1+w2*x2
代入x1,x2的取值,w1=w2=0.5,x0=1,则方程变为
w0*1+0.5*0+0.5*0<=0,求得w0<=0
w0*1+0.5*0+0.5*1<=0,求得w0<=-0.5
w0*1+0.5*1+0.5*0<=0,求得w0<=-0.5
w0*1+0.5*1+0.5*1>0,求得w0>-1
也就是说,在我们假定w1、w2权重都为0.5的情况下,联合以上w0的取值范围,表明只要-1<w0<=-0.5即可。也即-1<b<=0.5。b是什么,就是所谓的偏置,为了满足结果,神经元自己的权重偏好设置。偏置=偏好设置:D
假设我们令w0=-0.5,w1=w2=0.5我们看一下行不行。
x1=0,x2=0时 -0.5*1+0.5*0+0.5*0=-0.5,Sgn函数计算结果为0
x1=0,x2=1时 -0.5*1+0.5*0+0.5*1=0,Sgn函数计算结果为0
x1=1,x2=0时 -0.5*1+0.5*1+0.5*0=0,Sgn函数计算结果为0
x1=1,x2=1时 -0.5*1+0.5*1+0.5*1=0.5,Sgn函数计算结果为1
如我们所愿,正是and函数的结果。

封面
