范数等价性定理指在有限维空间中，不同的范数之间存在常数c1和c2，使得对于所有向量x，

有c1∣∣x∣∣q≤∣∣x∣∣p≤c2∣∣x∣∣q​成立，其中∣∣x∣∣p​和∣∣x∣∣q分别表示向量x在两种不同范数下的范数值。‌

这个定理的重要性在于，它表明在有限维空间中，尽管存在多种不同的范数定义方式，但这些范数在本质上是一致的。换句话说，无论我们选择哪种范数来度量向量的大小，得到的结果在数值上总是相近的。这一性质在矩阵代数的研究中尤为重要，因为在有限维空间（如矩阵空间）中，不同的范数研究效果是一致的，因此在实际应用中不区分范数的种类。

范数等价性定理的证明通常涉及到寻找两个范数之间的最大值和最小值，这些最大值和最小值可以用来构建上述不等式中的常数c1​和c2​。这一性质不仅适用于向量空间，也适用于矩阵空间，表明在有限维空间中，无论是向量还是矩阵，不同的范数定义方式在数学分析和应用中可以相互替代，而不影响最终的结果。这一点在泛函分析、线性代数以及相关的数学和工程领域中有着广泛的应用‌。

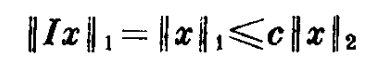
逆算子定理如下：