此前发布了两道小学五年级竞赛题:直角三角形斜边、两直角边之和或差已知,求其面积!这两道题,近乎清一色白卷,会做的寥寥数人,只有极个别同学会做!多数都在质疑严重超纲,并认为非使用勾股定理求解不可!
例1、斜边、两直角边之差已知!【贝笑题集】第553题: 如图,

图一
直角三角形ABC的斜边长为10,两直角边之差BC-AC=2,求其面积。
例2、斜边、两直角边之和已知!【贝笑题集】第426题:如图,

图二
直角三角形ABC的斜边长为10,两直角边之和AB+BC=14,求其面积。
适用知识:①简单勾股数,仍有超纲嫌疑!关于简单勾股数与勾股定理的区别,不再赘述!②拼图!
超纲知识:勾股定理,二元二次方程,平方和公式!
注:若使用勾股定理求解,还需解二元二次方程或使用平方和公式!
一、有超纲嫌疑的解析:简单勾股数!
仅适用于边长为整数情形。
例1的解析:注意到BC-AB=2及AC=10,依据三角形任意两边之和大于第三边,仅考虑BC和AB分别取整数值情形:9与7、8与6、7与5。与弦为10的简单勾股数进行对照,即知两直角边分别BC和AB分别为8与6。故S△ABC=6×8÷2=24。
例2的解析:注意到BC+AB=14及AC=10,依据三角形任意两边之和大于第三边,仅考虑BC和AB分别取整数值情形:9与5、8与6、7与7。与弦为10的简单勾股数进行对照,即知两直角边分别BC和AB分别为8与6。故S△ABC=6×8÷2=24。
简单勾股数求解的缺陷:
①只能说明直角边长8与6是唯一自然数解,尽管是唯一实数解,但无法说明或证明其实数解的唯一性。
②若要说明其边长8与6是唯一实数解,还需使用勾股定理,但超纲!
二、不超纲解析:拼图!
例1的解析:内图!
①用4个与△ABC相同的直角三角形拼成一个以斜边AC为边的大正方形、其边长为10,内含一个以BC-AB为边的小正方形、其边长为2。如图三
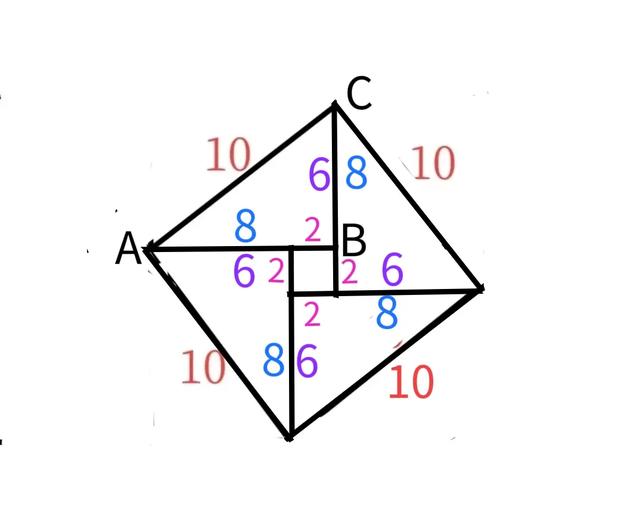
图三
②拼图规则:任意两个三角形的勾即短直角边、与股即长直角边交替对齐、重叠,剩余部分构成边长为2的小正方形!
③如图三,显然4S△ABC=S大正方形-S小正方形=10×10-2×2=96。故S△ABC=24。
例2的解析:外图!
①用4个与△ABC相同的直角三角形拼成一个以直角边和AB+BC为边的大正方形、其边长为14,内含一个以斜边AC为边的小正方形、其边长为10。如图四

图四
②拼图规则:任意两个三角形的勾即短直角边、与股即长直角边交替拼成大正方形的边!
③如图四,显然4S△ABC=S大正方形-S小正方形=14×14-10×10=96。故S△ABC=24。
—————————————————————
友友们有好的思路或方法,欢迎留言分享!

lanmaolanmao
给初中生做这样的题比较合适。初中生用完全平方公式和勾股定理来解答就比较合适了。
最是光阴化浮沫
原题相当于c=10,a+b=14,求ab/2。(a+b)²=a²+2ab+b²=14²,又因为a²+b²=c²,所以有2ab+10²=14²,可得ab/2=(14²-10²)/2=24,这才是初中正确的解法。
用户10xxx94 回复 05-08 22:58
我读书的时候,初中才学到勾股定理,现在勾股定理小学就学了吗?
只要你能吃苦那就会有吃不完的苦 回复 用户10xxx94 05-10 15:47
以前每个地方教材不一样的,我6年级拿奥数的题找老师,老师也说了得用初中的才解得了[笑着哭]
摸馍抹墨
选择题填空题直接套6,8,10,正常应用题那就x^2+(x+2)^2=100,慢慢解呗
亦香
知道勾股定理的小学生就会做这道题,当然平方和与差,小学生没学,但参加竞赛的小学生起码自学了初中数学。
村里买了直升机
一天到晚搞这种这种东西有啥意义?!
用户15xxx24
既然竟赛题,第一时间肯定拿345验证啦。过了就写,先得分,满不满分再说。做完回头再算。。谁会浪费时间
嗄呗 回复 05-16 09:15
可以先猜出结果,然后再证明这个结果是对的,这就可以了。[静静吃瓜]
用户38xxx61 回复 03-01 08:16
[笑着哭]你语文老师还好吗
momo
小编就是作作秀,自命不凡而已,这种题目对提高数学能力毫无卵用,最多算超前教育!
曼陀罗
本末倒置,一个简单的勾股定理就可以解出,何必非要整这些花里胡哨的东西?不要跟我说这是开发智力
路米
公式1:BC-AB=2 公式2:BC的平方+AB的平方=10的平方=100 那么(AB-BC)*(AB*BC)=4 公式3:AB的平方-2AB*BC+BC的平方=4 那么公式2-公式3=2AB*BC=100-4=96 AB*BC/2=96/4=24
用户62xxx51
拼图也是勾股定理,只不过不是直接用,是先自证再用
无无为
没有意义的教学
画葫 回复 04-04 08:54
考100分,就可以了
尼古拉屎
用尺子量,毕竟试卷上的图都是一样大小的[抠鼻]
杨百万在线
利用拼图求三角形面积是提高的标志
松燚遥
24,非常简单
麻核桃
两边只差的平方减去斜边的平方直接求
爱吃萝丝
数据必须满足经典比例,否则小学生做不出来
今时月
这种还解不出来,还读书干嘛?
大风起兮云飞扬
只要算AB和BC长度,一下就能算出面积
芽芽
不让留级以后会出现一大批新“文盲”。
yuhong88
现在知识点东一块西一块,不系统,就是各种做题,学生基础越来越差
jcx
勾三股四玄五嘛,要啥二元二次
老帅 回复 03-25 21:53
正确!
人间亚龙
既然说了是五年级了,直角边答案肯定是实数6和8
lff
反正面积是固定的,
开局一只碗
勾三股四弦五,各乘二。6,8,10
一天世界晴
勾股定理吗 勾三股四玄五
伟大的诚哥
6,8,10,秒了[得瑟]
锅底灰
拼接法。四个三角形组大正方形
六玥的风
235[得瑟]6810
税醒了
勾股定理对于一个敢参加数学竞赛的无论哪个年级的小学生,超纲吗?为啥非要脱裤子放屁呢?