此前发布了一道初中数学竞赛题:等腰三角形内一点与3个顶点连线共形成6个角,其中4个角的角度已知,求剩余2个角的角度!此题难度超大,班上全军覆没,学霸也不例外!10分钟内能做出来的同学,其高考数学成绩大概率140以上!
初中数学竞赛:如图一,

图一
P为三角形ABC内一点,连接PA、PB和PC,∠ABP=30°,∠PBC=40°,∠BCP=20°,∠ACP=50°,求∠PAC。
解析:需使用两次角平分线定理!
①过点A作BC的垂线AE,与BP的延长线相交于点D,连接CD,如图二

图二
②注意到∠ABC=∠ACB=70°,故△ABC为等腰三角形,从而其关于AE对称,也即有BD=CD,∠DCE=∠DBE=40°。
③∠DCP=∠DCE-∠BCP=20°=∠BCP,即CP为△BCD中∠BCD的角平分线。由角平分线定理可得BP/BC=PD/CD,即BC/CD=BP/PD。
④过点D作AC的垂线DF,如图三
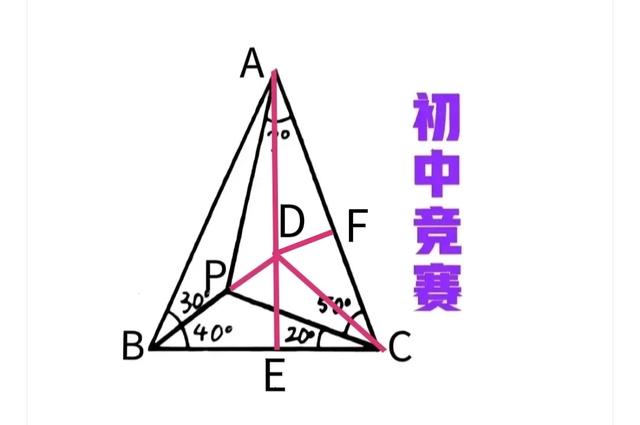
图三
⑤注意到∠DCF=∠ABD=30°,在直角三角形CDF中,30°角对应的直角边等于斜边的一半,即CD=2DF。
⑥S四边形ABDC=2S△ACD=DF×AC,另一方面,S四边形ABDC=AD×BC÷2。故AD×BC=2DF×AC=CD×AC,也即有BC/CD=AC/AD。
⑦注意到AB=AC,由④和⑥即知,BP/PD=BC/CD=AC/AD=AB/AD,再由角平分线定理可知,AP为∠BAD的角平分线。
⑧注意到∠BAE=∠CAE=20°,再由⑦即得∠BAP=∠DAP=10°。因此∠PAC=30°。
———————————————————
友友们有好的思路或方法,欢迎留言分享!

嗄呗
用正弦定理加三角函数很好做,不知道对于现在的初中生会不会超纲。
嗄呗
设所求角为α,0<α<40⁰;因为:AB/AP=AC/AP,所以:sin(70⁰-α)/sin30⁰=sin(50⁰+α)/sin50⁰⇔sin(70⁰-α)cos40⁰=sin((50⁰+α)/2)cos((50⁰+α)/2);代入:α=30⁰成立,则α=30⁰为方程的一个解;又由于P点的确定性,α在取值范围内唯一;综上所述:α=30⁰