此前发布了一道五年级数学题:九宫格内仅已知2个数,要填7个数,中心数、幻和均未知!咋求其所有解?由于仅给2个数,中心数取值可能不唯一,故其为不定三阶幻方!
五年级数学:依规律、填数!如图一,

图一
九宫格内已知“1”和“9”,请填入7个不重复自然数,使得每一行、每一列、每一条对角线上三数之和均相等。问:①共有多少个解?②请至少给出1个解!
解析:
1)先确定中心数的可能取值:8或10!
①第3列中间数可能取值≥0,记其为○。由第2行三数之和等于第3列三数之和、也即

图二
图二中两蓝线之和相等,可知中心数为1+9-○也即10-○,故中心数取值必≤10。
②第3行中间数可能取值≥0,记其为□。由主对角线上三数之和等于第3列三数之和、也即
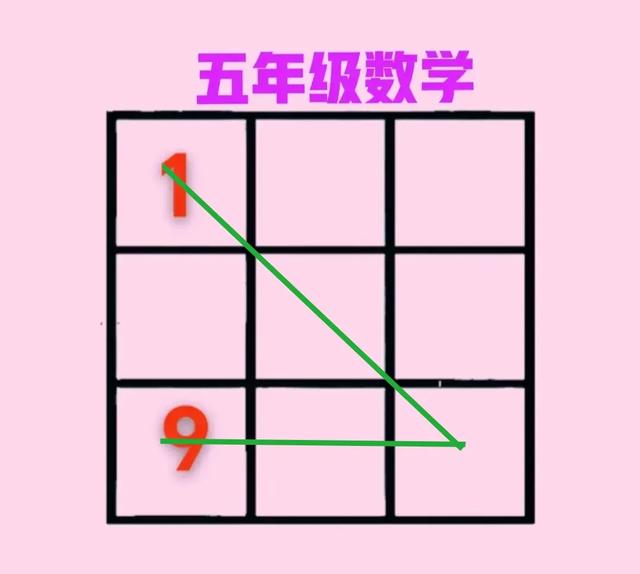
图三
图三中两绿线之和相等,可知中心数为9+□-1即8+□,故中心数取值必≥8。
③由①和②即知中心数可能取值有:8、9或10。再由不可重复性,中心数只有两种可能取值:8或10!
2)中心数取8时,有

图四
3)中心数取10时,有

图五
因此图一幻方共有2个解!
—————————————————
友友们有好的思路或方法,欢迎留言分享!
