零点问题是高考的热点问题,有关零点的问题常常与函数的单调性、极值点、最值等问题相关,有关零点的常见题型包括零点存在性的判定,零点个数的判定,零点取值区间的判定,多个零点相互关系的判定等等,其中有关两个零点之和的取值问题一般为极值点偏移问题的一种情形,而有关两个零点差的问题则主要考查两个零点之间的位置关系,即零点之间的距离。
函数最重要的一个性质为函数的单调性,利用导数研究函数的单调性是导数问题的最基本的问题,函数的极值点、最值、零点均与函数的单调性相关,而解决零点差问题其最根本的方法仍然是利用函数的单调性进行研究零点之间的相互关系。
今天老唐数学归纳总结了几个题目,对此类问题做一次思路上的解析。

▼
形式和极值点偏移问题并没太大区别,都属于函数构造的范畴,利用新函数的单调性和特殊值以及未知变量所处的单调区间来证明不等式成立,此时所证不等式形式一般较为简洁,不含分式或指对数的形式,如下题:





确定两变量各自的具体范围
▼
若已知函数中参数范围,则可将参数的范围看作其中某个变量的值域,再具体求出变量的范围即可,这种形式常常只需确定其中一个变量范围即可,或者根据函数单调性和特殊点直接判断出两个未知量的范围,典型案例如下:
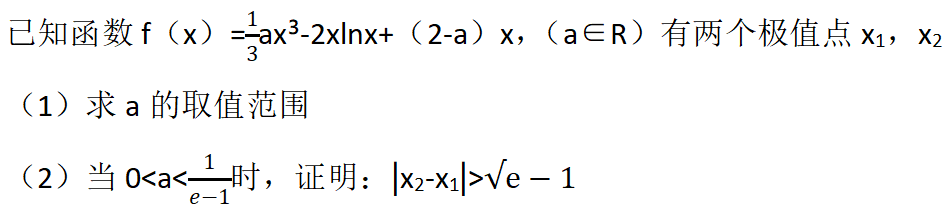


替换参数
▼





切割线放缩
▼




