
从e的极限定义开始:
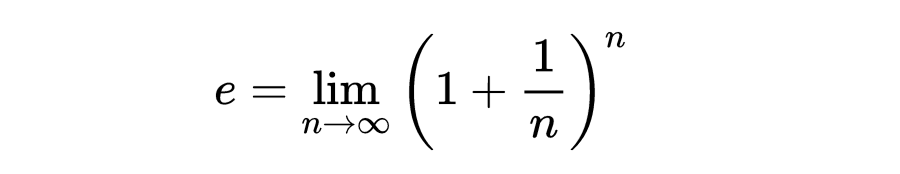
我们把它看成是r和s两个变量的实函数,用有理数r/s替换整数n。

r与s的比值越大,对e的近似就越好。
这个表达式可以用子函数f(x)替换r,用子函数g(x)替换s,从而把它重新定义为单变量复合函数。如果f(x)和g(x)是单调的和发散的,并且

那么:

现在,如果我们用适当的三角函数赋值f(x)和g(x),例如,我们可以设f(x)=cos(θ),g(x)=sin(θ)。当θ趋于π时,cos(θ)趋于-1,sin(θ)趋于0。虽然函数在θ=π处没有定义,但我们发现:

为了评估这类表达式的相对收敛速度,我们可以通过将θ替换为π±1/x,然后计算当x趋于无穷时的表达式,从而得到它们各自的幂级数。在这种情况下,当θ向右接近π时,我们有一个一阶近似:

输入π的前32位:
3.1415926535897932384626433832795
得到e的前32位:
2.7182818284590452353602874713526

cot(θ)函数图
现在我们看看让函数f(x)=cot(θ),g(x)=tan(θ)会发生什么。当θ向右趋于π时,cot(θ)趋于负无穷,tan(θ)趋于0。当θ向左趋于π时,cot(θ)趋于正无穷,tan(θ)趋于0。将这些函数代入,并使用三角恒等式:

从左接近π,得到一个二阶近似:

输入π的前32位:
3.1415926535897932384626433832795
得到e的前64位:
2.718281828459045235360287471352662497757247093699959574966967627
下面的一阶表达式有一个有趣的性质,它除了收敛于e之外( θ→π时),在5π/4处收敛于根号2,在3π/2处收敛于1。


三维散点图显示了7π/4 < θ < 11π/4的虚分量。复区域的模量在θ→2π时趋近于e。它在θ = 3π/4处无定义,在θ = 7π/4在π和2π处有可移奇点。
另外,三角函数替换并不是唯一方法。例如,只需稍加操作,我们就可以得到这个无限乘积:

当然,用π来计算数字e不是很实用。如果有笔和纸,那么用无穷级数会容易得多。尽管如此,这些表达式在几个世纪以来一直令数学家着迷,两个数字之间竟有一种意想不到的联系。

金老板
老胡不会不知道欧拉
拉夫
e的派i次幂=1
用户16xxx03 回复 07-01 23:23
-1
用户15xxx35
老胡连欧拉公式都不知道也敢说e与兀关系
用户14xxx08 回复 07-12 18:11
你觉得做数学科普的会不知道欧拉公式?
路见不平躲着走 回复 08-27 11:09
你用欧拉公式给我算出e的值来
元道
好
好色贪财一身正气
欧拉在默默看着
白莲圣上
e就是按π整出来的
徐春海
好文章。
欧阳锋
学习胡老师的文章开阔思路。
天骄
[吃瓜]