此前发布了一道五年级数学竞赛题:梯形被分成3个三角形,其中2个面积已知,求另一个三角形面积!真没想到,竟然被“团灭”,学霸也不例外!难度非常大,不超纲求解,家长也摇头!割补法,或可迎刃而解!
如图一,
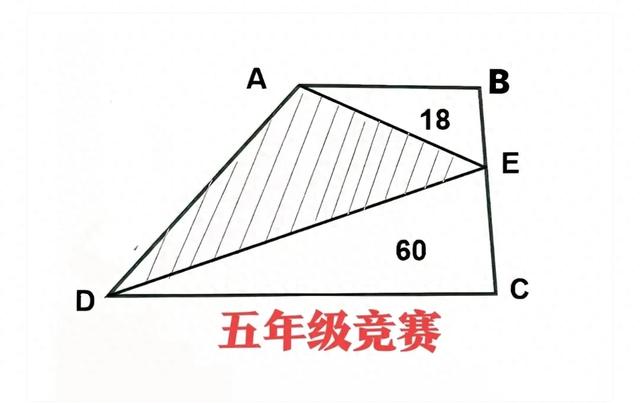
图一
E为梯形ABCD腰BC上一点,CD=2AB,三角形ABE和CDE的面积分别为18和60,求阴影部分三角形ADE的面积。
不少家长朋友偏好利用代数运算求解,的确简单!但五年级没学代数运算!
超纲解析:代数法!
①分别记△ABE底边AB和△CDE底边CD上的高为h₁和h₂,由三角形面积公式可得AB×h₁=36,2×AB×h₂=CD×h₂=120。
②由梯形面积公式及乘法分配律,可得S梯形ABCD=(AB+CD)×(h₁+h₂)÷2=(3×AB×h₁+3×AB×h₂)÷2
=(108+180)÷2=144。
因此,S△ADE=144-18-60=66。
不超纲解析之一:割补法!
①补齐平行四边形BCDF,过点D作CB的平行线,与BA的延长线相交于点F。过点E作CD的平行线交DF与点G,过点A作BC的平行,分别与EG、CD相交于点O和点H,连接OD。如图二

图二
②注意到A、H分别为BF和CD的中点,由同(等)底等高三角形面积相等,可得S△AOD=S△AOF=S△AOE=S△ABE=18,S△DOE=1/2S△CDE=30。
③S△ADE=S△AOD+S△AOE+S△DOE=18+18+30=66。
不超纲解析之二:分割法!
①过点A作BC的平行,与CD相交于点F,连接EF。如图三

图三
②显然,F为CD的中点,故S△CEF=60÷2=30。从而S平行四边形ABCF=(30+18)×2=96,S△ADF=1/2S平行四边形ABCF=48。
③S梯形=96+48=144,从而S△ADE==144-18-60=66。
———————————————
友友们有好的想法或思路,欢迎留言分享!

无为而为
连接bd,可知3角形bde的面积为36,3角形d bc的面积为60+36=96。a bd的面积为dbc的一半48。ade面积等于48+36-18=66
JYYX
BE/EC=18✘2/60=3/5 18/(3/(3+5))=48 60/(5/(3+5))=96 (48+96)-60-18=66
用户73xxx63
连接AC。S△ACE=1/2S△CED=30,S△ABC=30+18=48, S△ACD=2S△ABC=96, 梯形面积=96+48=144, S△ADE=144-60-18=66。