正确率不及5%!填空题的缘故,很多不会做的同学就侥幸“蒙”一下,很可惜答案是无理数,结果可想而知,一个蒙对的也没有!这是一道初中数学竞赛填空题:如图一,
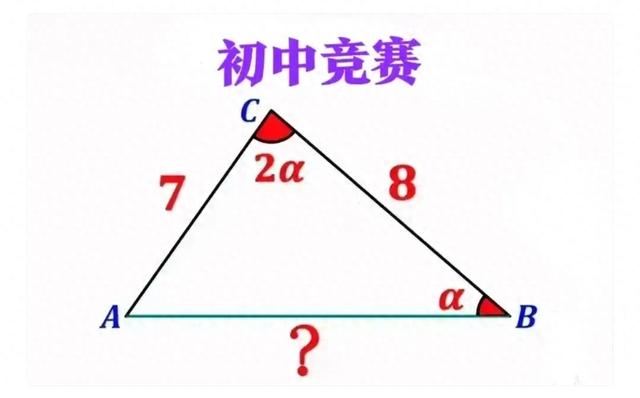
图一
在三角形ABC中,∠ACB=2∠ABC,AC=7,BC=8,求AB长。
主要考查:①角平分线定理②三角形相似、全等③勾股定理等!
一、不超纲解析之一:角平分线定理+三角形相似!适合初中生
①作∠ACB的角平分线CD与AB相交于点D,如图二

图二
②显然,∠ACD=∠BCD=∠ABC=α,∠ACB=∠ADC=2α,故CD=BD。
③令AB=a,由角平分线定理AC/AD=BC/BD,故CD=BD=8a/15。
④显然△ABC与△ACD相似,故AC/AB=CD/BC,也即8a²/15=56。因此,a=√105。
二、不超纲解析之二:三角形全等+勾股定理!适合初中生
①将图二中角平分线CD延长至点E,使得AC=AE=7,连接BE,过点A作BC的垂线AF,如图三

图三
注1:若∠ACB为钝角,则过点C作AE的垂线即可!
②显然,
∠ACD=∠BCD=∠ABC=∠AEC=∠EAD=α,∠ACB=∠ADC=2α。故AE⫽BC,AEBC为一梯形。
③△ACD≌△EBD,故AC=EB=7,从而AEBC为一等腰梯形。
④由③即知CF=1/2,BF=7.5。
⑤由勾股定理可得AB²=AF²+BF²=AC²-CF²+BF²=7²-0.5²+7.5²=105,也即AB=√105。
注2:即便AC和BC未知,由BF=AE+CF=AC+CF=BC-CF,从不超纲解析之二步骤⑤出发,利用平方差公式,可推导出如下公式,
AB²=AC²-CF²+BF²=AC²+(BF-CF)(BF+CF)=AC²+AC×BC。
—————————————
友友们有啥想法或思路,欢迎留言分享!

煅剑
方法不好。
用户10xxx19
相似三角形对应边的比相等 即可求出ad与bd的关系 可解二元二次方程 得出答案
用户10xxx08
倍角相似不就行了。。
用户10xxx97
方法太菜!
昨日牵绊
因为7<8 所以角A大于角B 过A点画线 交BC于H.使角HAB等于角B 这样角CHA刚好是2倍角B 在三角型ACH中 AC=AH=7 CH=CB-CH=CB-AH=1 直接求了
小新
这题简单题啊,不应该出在竞赛题当中啊
Jay
就这也是竞赛题[捂脸哭][捂脸哭]
为爱寻找
∠A=π-3a,SIN(π-3a)=SIN(3a)=3SINa-4(SINa)的立方,根据正弦定理7/SIN(B)=8/SIN(A),即7/SINa=8/3SINa-4SINa的立方,解得SINa等于多少就省略了,求的SINa以后,再求COS(2a),然后用余弦定理求AB长,
看啥不是啥
不会很正常啊,会了派什么用?说说看吗?
语很鱼
是想证明只有聪明人才能做呢?还是说这类题目做了能聪明起来???
Free
[点赞]
用户14xxx91
这题就是相似三角形,不难吧
科研小达人
CA*CB*sin(2a) = CA*AB*sin(180-3a) = AB*CB*sina
用户12xxx76 回复 08-13 23:52
角未知,你算个得。
星云彼岸 回复 用户12xxx76 08-30 16:03
[吃瓜]能算出来的,倍角公式一代入进去就行了,然后求方程组解