与茂名湛江同一州进行二模考试的还有梅州，只是梅州的单选第8题是一道错题，所以之前没有讲。

这份卷子整体来说难度倒是不大，即使是各个压轴题中等学生也都能做一做。

八道单选题

首先是第三题是之前考过几次的题，三个函数与直线的交点，数形结合比较大小。

其次是第4题，这一题出得不太好，毕竟有一部分同学没有选物理。而这道题对没有选物理的同学，不太公平。

第5到第7题也都是基础难度的题。

第8题的a和c选项都是对的，所以这道题出错了。但如果不是选项出错了，此题倒是一道不错的圆锥曲线小题。建议大家当填空题再做一做。

三道多选题——此份试卷的多选题出得还可以。

第9题是复数的基础计算题

第10题是一道较好的数列多选题，关键点是对b选项的计算判断

第11题也是一道很不错的立体几何压轴题，a选项比较简单，利用勾股定理计算出截面圆的半径；b选项明显是一个面，c选项和d选项相对较难，c选项首先要能理解到直线MN的距离为1的点的轨迹是一个圆柱，d选项中满足∠MNP等于45度的点的轨迹是一个圆锥，则这两个选项就好判断了，分别为圆柱与阿尔法这个平面的交线，以及圆锥与阿尔法这个平面的交线。

三道填空题

第13题假如不会做，就多求几项来比较趋势，也能得到正确答案。

第14题则是一道以往考过的曼哈顿距离的题，本质上是绝对值函数问题，数形结合即可解决。所以，本次考试的填空题是没有难度的。

五道大题

第15题是圆锥曲线的送分题。

第16题也是一道基础难度的题，但第3问的模型比较重要，经常考到。利用互补角的余弦之和为零构建方程，在解三角形的题中经常用到设未知数利用正余弦定理构建方程来求解。

第17题是一道中等难度的例题，几何好题。第2问和第3问都与近期其他模拟卷中的几何题不太一样，这两问以往更多的是除填空题。

第18题是一道导数中档题，第2问求零点个数是道直接用分类讨论法求解的典型例题。

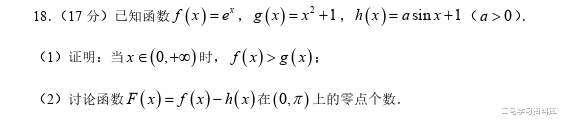
第19题是一道数列创新压轴题，难度不算大，第一问是送分题。第2问和第3问都是抽象的逻辑推理，但不算难。使用作差法和题目所给的生成数列的定义即可证明。第三问需要对pn这个数列是否为常数数列进行分类讨论，这样难度的压轴题，对于想考高分的考生来说，是有必要突破的。

最后，给大家发下参考答案，同学们可以练习一下。