§4.7利用二次函数的图象解一元二次不等式
在第一章里,我们曾经学过利用因式分解的方法解一元二次不等式。例如,要解不等式
x²-2x-3<0. (1)
可以先把二次三项式x²-2x-3分解成因式,得到
( x +1)( x -3)<0.
由此可以知道不等式的解是
-1<x<3.
用同样的方法,我们还可
以知道,不等式
x²-2x-3>0 (2)
的解是
x <-1和 x>3.
这两个不等式的解,我们也可以从二次函数
y=x²-2x-3
的图象(图4.21)上看出来.

在图里,抛物线 y=x²-2x-3和 x 轴交于两点 A (-1,0), B (3,0)。我们看出,当x取大于﹣1而小于3的值的时候,图象在x轴的下方,这时的函数值是负数,就是
x²-2x-3<0,
因此﹣1<x<3是不等式(1)的解。我们还看出,当 x 取小于-1或者取大于3的值的时候,图象都是在x轴的上方。这时函数所对应的值都是正数,就是
x²-2x-3>0,
因此 x <-1和 x>3是不等式(2)的解。
利用函数的图象解不等式,叫做不等式的图象解法.
例1.利用图象解不等式
2-2x-x²>0.
【解】用﹣1乘不等式的两边,得到
x²+2x-2<0.
作函数 y=x²+2x-2的图象(图4.22).
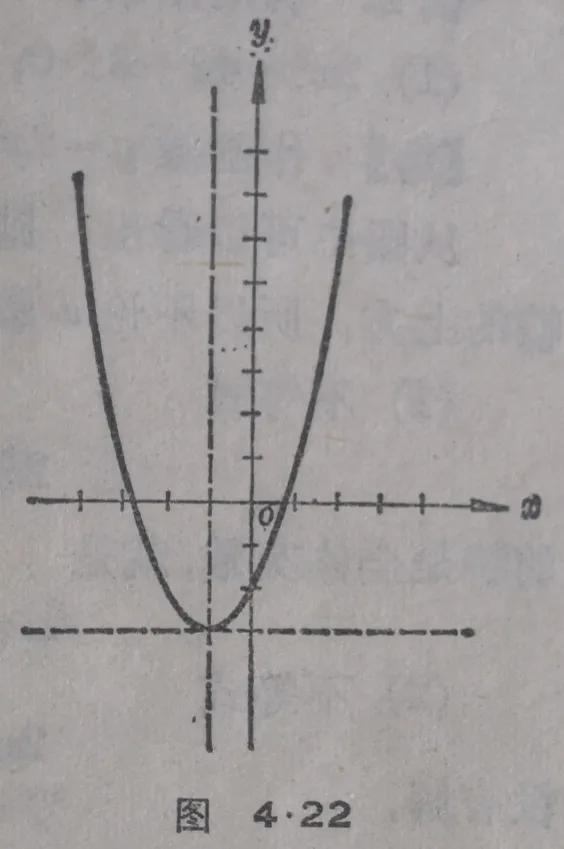
从图中可以看出,抛物线与x轴相交于两点,它们的横坐标
x₁≈-2.7, x₂≈0.7.
当 x 取大于-2.7而小于0.7的值的时候,图象在x轴的下方,这时
x²+2x-2<0.
因此原不等式的解是-2.7<x<0.7.
注 利用图象法解不等式,在一般情况得到的解只是近似的。
这个不等式,也可以利用因式分解的方法来解。首先我们求出方程x²+2x-2=0的两个根.
x₁=-1-√3(≈-2.7321),
x₂=-1+√3(≈0.7321).
这样,原不等式可以改写成
[x-(-1-√3)][x-(-1+√3)]<0
这个不等式的解是
-1-√3<x<-1+√3。
例2.利用图象解不等式:
(1) 2x²-4x+3>0;
(2) 2x²-4x+3<0.
【解】作函数 y =2x²-4x+3的图象(图4·23)。

从图中可以看出,抛物线始终不和x轴相交,并且x轴的上方,所以不论 x 取什么实数值,总有 y>0.因此;
(1)不等式
2x²-4x+3>0
的解是全体实数,就是
-∞<x<+∞
(2)不等式
2x²-4x+3<0
没有解.
例3.利用图象解不等式:(1)4x²-4x+1>0;
(2)4x²-4x+1<0.
【解】作函数 y =4x2-40+1的图象(图4.24)

从图中可以看出,当 x =½的时候,y=0.当x≠½的时候,y>0. 因此:
(1)不等式
4x²-4x+1>0
的解是除去½以外的全体实数,就是
x <½ 或者 x>½.
(2)不等式
4x²-4x+1<0
没有解。
习题4.7
利用二次函数的图象解下面这些不等式:
1. x²-3x+2>0.
2. 2x²-3x+1<0.
3. x²+ x +1>0.
4. x²- x +1<0.
5. 1+ x -x²>0.
6. 1- x -x²<0.
下期预告:
*§4·8一元二次不等式的解的讨论
在§4.7的这些例题中,可以看到一元二次不等式的解可以有三种情况:
(1)它的解是某些范围内的实数;
(2)它的解是全体实数;
(3)它没有解.
现在,我们来研究怎样象判别一元二次方程
ax²+ bx + c =0( a ≠0)
......
上期链接:
https://m.toutiao.com/is/ircUvN7c/ - 百科漫谈:名师彻底讲透初等函数(20)利用二次函数的图象解一元二次方程 - 今日头条

