​​

此前发布了一道五年级竞赛题：三角形仅一边已知、高未知，求其面积！不少同学反映，此题太难了，非使用超纲知识三角形全等不可。还有同学认为，此题缺少条件、无法求解！

五年级竞赛题：如图一，

图一

ABCD为正方形，AE垂直EF，CF垂直EF，BF=8，求红色阴影部分三角形ABF的面积。

注意到，此题只有一个数字条件BF=8！特别地，AE未告知！这是不少同学自然地认为“缺少条件、无法求解”的原因所在！

关键问题：说明或证明△ABF的底边BF上的外高AE=BF！

超纲解析：适合初中生，三角形全等！

易知∠EAB=∠FBC，∠EBA=∠FCB，且AB=BC，从而由角边角判定可知△AEB≌△BFC，故AE=BF=8。因此S△ABF=8×8÷2=32。

不超纲解析：适合小学生，图形旋转！

①将△ABE绕点B顺时针旋转90°至BA与BC重合，旋转后的△ABE记为BCE'。如图二

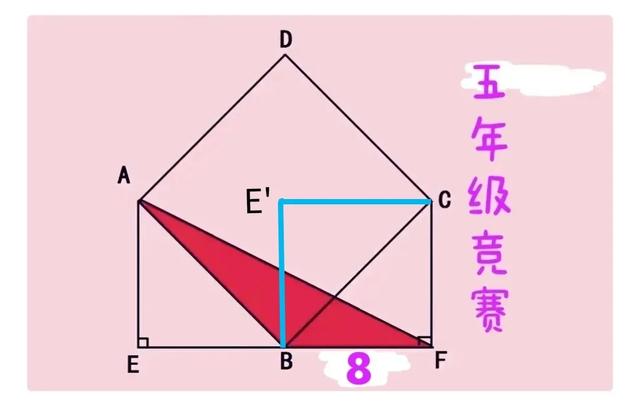
图二

②显然，∠BE'C=∠FBE'=90°，∠BCE'=∠BAE，BE=BE'，CE'=AE。

③注意到∠ABE+∠CBF=90°，故∠BAE+∠BCF=90°，从而由②可得，∠FCE'=∠BCE'+∠BCF=90°。

④由②和③即知，四边形BE'CF为长方形。从而其对边相等，即CE'=BF=8，BE'=CF。再由②中AE=CE'，可得AE=BF=8。如图三

图三

⑤因此，S△ABF=AE×BF÷2=32。

—————————————————

友友们有好的思路或方法，欢迎留言分享！