史永鑫
一、晶体结构的基本考查角度
1. 晶胞中微粒数(包括化学式)的计算方法——均摊法(如图1)

非平行六面体形晶胞中粒子数目的计算同样可用“均摊法”,其关键仍然是确定一个粒子为几个晶胞所共有。
2.立方晶胞中,晶胞棱长a与原子半径r的关系(以金属晶体为例)
(1)简单立方堆积:棱长a=2r。
(2)体心立方堆积:体对角线长为 3 a=4r 。
(3)面心立方最密堆积:面对角线长为 2 a=4r 。
3. 配位数(以金属晶体为例)
(1)简单立方堆积:6。
(2)体心立方堆积:8。
(3)六方最密堆积:12。
(4)面心立方最密堆积:12。
4. 晶体密度
ρ= Ν×Μ a 3 Ν A (a 表示立方晶胞边长,ρ表示密度,NA表示阿伏加德罗常数,N表示1个晶胞所含基本粒子或特定组合的个数,M表示摩尔质量)。一定要注意单位换算。
5. 晶胞中原子的空间利用率(或占有率)
空间利用率 = 晶胞占有的微粒体积 晶胞体积 ×100%
6. 晶胞中原子的分数坐标
(1)原子分数坐标:以晶胞参数为单位长度(不论晶胞边长大小,都是1)建立的坐标系。晶胞中的任意一个原子的中心位置均可用3个分别<1的分数在立体坐标系中表示出来。
(2)确定某原子分数坐标的方法:通过该原子可以作出三个平行于坐标轴的平面,三个平面在三条坐标轴上的截距占晶胞边长的分数,即该原子的分数坐标,如图2所示。
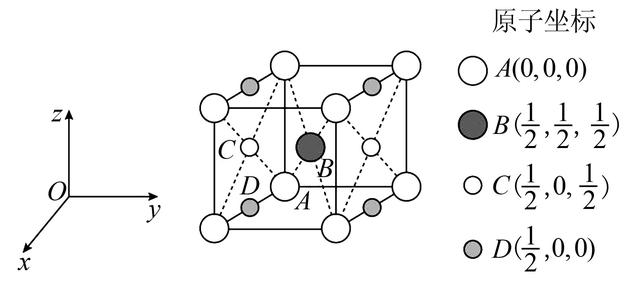
(3)在确定各原子的坐标时,要注意x、y、z轴的单位标准不一定相同。
7. 晶体的空隙类型
(1)粒子围成的四面体空隙。
(2)粒子围成的八面体空隙等。
二、常见典型的晶体结构及分析
1. 氯化钠(NaCl)(如图3)

(1)晶胞中Na+和Cl-的位置:Na+位于面心和顶点,Cl-位于体心和棱心,或反之。
(2)每个晶胞中Na+个数:8×1/8+6×1/2=4,Cl-个数:12×1/4 + 1 =4。
(3)晶胞中每个Na+周围等距且紧邻的Na+有12个,每个Cl-周围等距且紧邻的Cl-有12个。
(4)晶胞中每个Cl-周围等距且紧邻的Na+有6个,每个Na+周围等距且紧邻的Cl-有6个,即阴、阳离子的配位数均为6。
2. 氯化铯(CsCl)(如图4)

(1)晶胞中Cs+和Cl-的位置:Cs+位于顶点,Cl-位于体心,或反之。
(2)每个晶胞中Cs+个数:8×1/8=1,Cl-个数:1。
(3)晶胞中每个Cs+周围等距且紧邻的Cs+有6个,每个Cl-周围等距且紧邻的Cl-有6个。
(4)晶胞中每个Cl-周围等距且紧邻的Cs+有8个,每个Cs+周围等距且紧邻的Cl-有8个,即阴、阳离子的配位数均为8。
3.氟化钙(CaF2) (如图5)

(1)晶胞中Ca2+和F-的位置:Ca2+位于面心和顶点,F-位于晶胞内8个小立方体的体心。
(2)每个晶胞中Ca2+个数:8×1/8+6×1/2=4,F-个数:8。
(3)晶胞中每个Ca2+周围等距且紧邻的Ca2+有12个,每个F-周围等距且紧邻的F-有6个。
(4)晶胞中每个F-周围等距且紧邻的Ca2+有4个,每个Ca2+周围等距且紧邻的F-有8个,即Ca2+的配位数为8,F-的配位数为4。
4. 金刚石(如图6)

(1)每个碳原子与相邻的4个碳原子以共价键结合,形成正四面体结构。
(2)键角均为109°28′。
(3)最小碳环由6个C组成且6个原子不在同一平面内。
(4)每个C参与4条C—C键的形成,C原子数与C—C键数之比为1∶2。
(5)晶胞内部碳原子的位置:4个碳原子位于4个互不相邻小立方体的体心。
(6)晶胞中碳原子个数:8×1/8+6×1/2+4=8。
(7)配位数:4。
5. 二氧化硅(SiO2)(如图7)

(1)每个Si与4个O以共价键结合,形成正四面体结构。
(2)每个正四面体占有1个Si, 4个 “ 1 2 Ο”, n(Si)∶n(Ο) =1∶2 。
(3)最小环上有12个原子,即6个O、6个Si。
6.石墨(如图8)

石墨层状晶体中,层与层之间的作用是分子间作用力,平均每个正六边形拥有的碳原子个数是2,C采取的杂化方式是sp2杂化。
7.干冰(如图9)

(1)晶胞中4个CO2分子位于立方体8个顶点和6个面心。
(2)每个CO2分子周围等距且紧邻的CO2分子有12个。
三、真题赏析
例1(2014·海南卷节选)金刚石晶胞如图10,其中含有__个碳原子。若碳原子半径为r,金刚石晶胞的边长为a,根据硬球接触模型,则r=__a,列式表示碳原子在晶胞中的空间占有率__(不要求计算结果)。
解析 由金刚石的晶胞结构可知,晶胞内部有4个C原子,面心上有6个C原子,顶点有8个C原子,所以金刚石晶胞中C原子数目为 4+6× 1 2 +8× 1 8 =8 ;若C原子半径为r,金刚石晶胞的边长为a,根据硬球接触模型,则正方体对角线长度的 1 4 就是C—C键的键长,即 3 4 a=2r ,所以 r= 3 8 a ;碳原子在晶胞中的空间占有率为 8× 4 3 πr 3 a 3 = 8× 4 3 π×( 3 8 a) 3 a 3 = 3 π 16 。

答案: 8 3 8 3 π 16
点评 本题主要考查金刚石晶胞,包括均摊法求原子个数、晶胞棱长a与原子半径r的关系、原子的空间占有率等基本知识点。
例2 (2021·山东卷节选)非金属氟化物在生产、生活和科研中应用广泛。回答下列问题:

XeF2晶体属四方晶系,晶胞参数如图11所示,晶胞棱边夹角均为90°,该晶胞中有__个XeF2分子。以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置,称为原子的分数坐标,如A点原子的分数坐标为 ( 1 2 , 1 2 , 1 2 ) 。已知Xe—F键长为r pm, 则B点原子的分数坐标为__;晶胞中A、B间距离d=__pm。
解析 图中大球的个数为 8× 1 8 +1=2 ,小球的个数为 8× 1 4 +2=4 ,根据XeF2的原子个数比可知大球是Xe原子,小球是F原子,该晶胞中有2个XeF2分子;由A点坐标可知该原子位于晶胞的体心,且每个坐标系的单位长度都记为1,B点在棱的 r c 处,其分数坐标为 (0,0, r c ); 图中y是底面对角线的一半, y= 2 2 a, x= c 2 -r ,所以 d= x 2 +y 2 = 1 2 a 2 +( c 2 -r) 2 pm.
答案: 2 (0,0, r c ) 1 2 a 2 +( c 2 -r) 2
点评 本题主要考查均摊法求原子个数、原子的分数坐标以及对晶胞的结构分析等知识。
例3 Zn与S形成某种化合物的晶胞如图12所示。

(1)以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的位置,称作原子分数坐标。图中原子1的坐标为(0,0,0),则原子2的坐标为__。
(2)已知晶体密度为d g·cm-3,S2-半径为r(S2-)pm, 若要使S2-、Zn2+相切,则Zn2+半径r(Zn2+)为__pm(写计算表达式)。
解析 (1)由晶胞中各原子的相对位置关系容易推导出原子2的坐标为 ( 1 2 ,0, 1 2 ) 。
(2)已知晶体密度为d g·cm-3,锌离子的个数为 8× 1 4 +6× 1 2 =4 ,硫离子位于晶胞内部,个数为4,则晶胞参数为a,则 d= 4Μ(ΖnS) Ν A a 3 ,a= 4×65+32×4 dΝ A 3 ×10 10 pm= 388 dΝ A 3 ×10 10 pm, 若要使S2-、Zn2+相切,则其体对角线长度为1个锌离子半径与1个硫离子半径之和的4倍,即 3 a= 4[r(Ζn 2+ )+r(S 2- )],Ζn 2+ 离子半径 r(Ζn 2+ )= 3 × 388 dΝ A 3 ×10 10 -4r(S 2- ) 4 pm=[ 3 4 × 388 dΝ A 3 ×10 10 -r(S 2- )]pm
点评 本题主要考查原子的分数坐标、对晶胞的结构分析以及有关晶体密度的计算等知识。
例4 请回答下列问题:
(1)一种由铁、碳形成的间隙化合物的晶体结构如图13甲所示,其中碳原子位于铁原子形成的八面体的中心,每个铁原子又为两个八面体共用,则该化合物的化学式为__。

(2)电石(CaC2)是制备氯化氰(ClCN)的重要原料。四方相碳化钙(CaC2)的晶胞结构如图13乙所示,其晶胞参数分别为a、b、c,且a=b,c=640pm。已知四方相碳化钙的密度为1.85 g·cm-3,[C≡C]2-中键长为120pm。则成键的碳原子与钙原子的距离为__pm和__pm。(设阿伏加德罗常数的数值为6×1023)
解析 (1)每个八面体中包含了一个C原子,一共6个Fe, 每个Fe被两个八面体共用,所以化学式为Fe3C;
(2)侧面碳原子与钙原子的距离 c-120pm 2 = 640pm-120pm 2 =260 pm, 一个晶胞中包含了Ca: 1+8×1/8=2,C2:2×1/2+4×1/4=2,一个晶胞中包含了2个CaC2,所以一个晶胞的质量为: m= 2Μ(CaC 2 ) Ν A = 2×64 6×10 23 ,又因为 ρ= m V = m abc×10 -30 = m b 2 c×10 -30 ,可以求出 b= m cρ×10 -30 ;设距底面中心最近的碳原子与钙原子的距离为l,则 l 2 = ( 2 2 b) 2 +( 120pm 2 ) 2 ,解得l=306 pm。
答案: (1)Fe3C (2)260 306。
点评 本题主要考查均摊法求原子个数(化学式)、涉及了晶体结构的分析以及逆向考查了晶体密度的计算等。
例5 钴蓝晶体结构如图14,该立方晶胞由4个Ⅰ型和4个Ⅱ型小立方体构成,其化学式为__,晶体中Al3+占据O2-形成的__(填“四面体空隙”或“八面体空隙”)。NA为阿伏加德罗常数的值,钴蓝晶体的密度为__g·cm-3(列计算式)。

解析 根据钴蓝晶体晶胞结构分析,一个晶胞中含有的Co、Al、O个数分别为: 4×(4× 1 8 +2× 1 4 +1)=8,4×4=16,8×4=32 ,所以化学式为CoAl2O4;根据结构观察,晶体中Al3+占据O2-形成的八面体空隙;该晶胞的体积为(2a×10-7)3 cm3,该晶胞的质量为 8×(59+2×27+4×16) Ν A g ,所以密度为 8×(59+2×27+4×16) Ν A ×(2a×10 -7 ) 3 g⋅cm - 3 。
答案: CoAl2O4 八面体空隙 8×(59+2×27+4×16) Ν A ⋅(2a×10 -7 ) 3 。
点评 本题主要考查原子个数(化学式)的计算、晶体的空隙类型以及晶体密度的计算等知识点。




