主要内容:
本文主要介绍根式复合函数y=√[10+√(31-3x)]的定义域、单调性、凸凹性、极限等性质,并通过导数知识解析函数的单调区间和凸凹区间,同时简要画出函数的图像示意图。

对于根式函数y=√[10+√(31-3x)],要求为非负数,所以有:
31-3x≥0,即x≤31/3≈10.33,
则函数的定义域为:(-∞,31/3]。
※.函数的单调性两种思路来解析函数的单调性。
(1)函数单调性法
该函数y=√[10+√(31-3x)]由以下函数复合函数,即:
y=√u,u=10+√v,v=31-3x,
其中v为一次函数,且为减函数,则u=10+√v也为减函数,进一步知y在定义域上也为减函数。

(2)函数导数法:
根式函数y=√[10+√(31-3x)],对x求导有:
dy/dx=(10+√(31-3x)) '/2√[10+√(31-3x)]
=-(3/2√(31-3x)) /2√[10+√(31-3x)]
=-3/[4√(31-3x)*√(10+√31-3x)]<0,
所以函数y为减函数。
※.函数的凸凹性∵dy/dx=-3/[4√(31-3x)*√(10+√(31-3x)]
∴d^2y/dx^2=(3/4)*[√(31-3x)*√(10+√(31-3x)] '/[(31-3x)( 10+√(31-3x)],
=(3/4)*[-3√(10+√(31-3x)/2√(31-3x)+√(31-3x)* (√(31-3x)'/2√(10+√(31-3x)] /[(31-3x)( 10+√(31-3x)],
=-(9/16)[20+√(31-3x)]/ √[(31-3x)( 10+√(31-3x)]^3<0.
所以函数为凸函数。

lim(x→31/3) √(10+√(31-3x))= √10;
lim(x→0) √[10+√(31-3x)]=√(10+√31);
lim(x→-∞) √[10+√(31-3x)]=+∞。
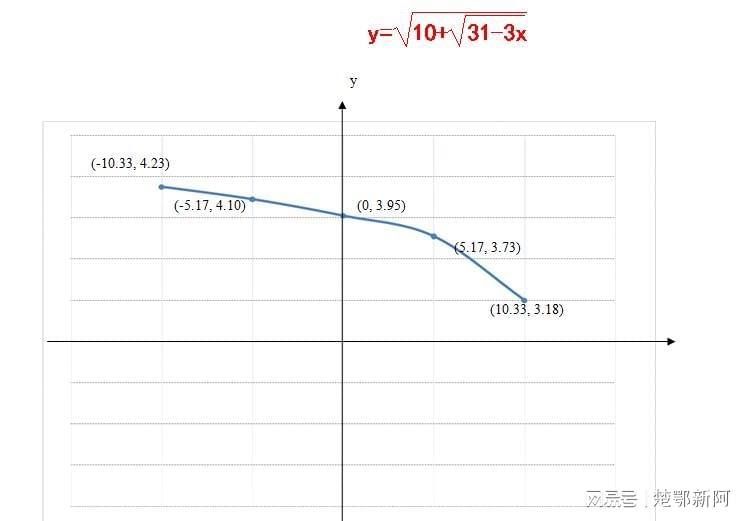
※.函数的五点图