摘要：前所未有的无监督训练（unsupervised training）数据以及神经缩放规律（neural scaling laws），导致模型规模和服务/训练 LLM 的计算需求空前激增。然而，主要的性能瓶颈正日益转向内存带宽。

在过去 20 年中，服务器硬件 FLOPS 峰值以 3.0 倍/2 年的速度增长，超过了 DRAM 和互连带宽的增长速度，而 DRAM 和互连带宽的增长速度分别仅为 1.6 倍/2 年和 1.4 倍/2 年。这种差距使内存而非计算成为人工智能应用的主要瓶颈，尤其是在服务领域。

在此，我们分析了编码器和解码器 Transformer 模型，并展示了内存带宽如何成为解码器模型的主要瓶颈。我们主张重新设计模型架构、训练和部署策略，以克服内存限制。

引言

最近，训练大型语言模型（LLM）所需的计算量以 750×/2 年的速度增长。这种指数级增长趋势是人工智能加速器的主要驱动力，这些加速器专注于提高硬件的峰值计算能力，往往以简化内存层次结构等其他部分为代价。

然而，这些趋势忽略了训练和服务人工智能模型的一个新挑战：内存和通信瓶颈。事实上，一些人工智能应用的瓶颈正在于芯片内/芯片间（intra/inter-chip）以及人工智能加速器之间的通信，而不是计算。这并不是什么新现象，过去就有一些著作观察到了这一问题并提出了警告。最早的一次观察可以追溯到 1990 年，当时 Ousterhout 在分析了影响操作系统性能的因素后得出了以下结论：

"第一个与硬件相关的问题是内存带宽：基准测试表明，内存带宽跟不上 CPU 的速度......"。如果未来机器的内存带宽不能显著提高，某些类别的应用程序可能会受到内存性能的限制"。

后来在 1995 年，威廉-伍尔夫（William Wulf ）和萨莉-麦基（Sally Mckee）进一步回应了这一预测，并创造了 "内存墙 "（memory wall）一词。他们的论证遵循一个简单而优雅的原理。完成一个操作所需的时间取决于我们执行运算的速度，以及我们向硬件运算单元提供数据的速度。

根据这一假设，即使 80% 的数据在高速缓存中随时可用，而只需从 DRAM 中获取 20%，但如果从 DRAM 中获取 20% 的高速缓存遗漏数据所需的时间超过 5 个周期，则完成运算的时间将完全受限于 DRAM。

这意味着，无论硬件每秒的运算速度有多快，问题都将完全受到 DRAM 带宽的限制。他们预测，执行计算的速度与获取数据的速度之间的差异将导致 "内存墙 "问题。据此，他们得出结论

"每种技术都在以指数形式不断进步，但微处理器的指数远远大于 DRAM 的指数。不同指数之间的差异也呈指数增长"。

后来的一些研究也报告了类似的观察结果。

在这项工作中，我们通过研究更近期的数据重新审视了这一趋势，尤其关注用于训练人工智能模型的硬件，以及用于训练/服务这些模型的计算的特点。30 年后，上述观察和预测再正确不过了。尽管内存技术出现了许多创新，但趋势表明，"内存墙 "正日益成为一系列人工智能任务的主要瓶颈。

我们首先分析自 1998 年 Yann Lecun 在 MNIST 数据上训练著名的 Lenet-5 模型以来，服务器级人工智能硬件的峰值计算量发生了怎样的变化。我们可以看到，在过去的 20 年中，硬件的峰值计算量增长了 60,000 倍，而 DRAM 的增长为 100 倍，互连带宽的增长为 30 倍。

内存墙问题既涉及有限的容量、内存传输带宽，也涉及其延迟（比带宽更难改善）。这需要不同层次的内存数据传输。例如，计算逻辑与片上内存之间的数据传输，或计算逻辑与 DRAM 内存之间的数据传输，或不同sockets上不同处理器之间的数据传输。在所有这些情况下，数据传输的容量和速度都明显落后于硬件计算能力。

现在，如果我们研究一下最近的人工智能模型，特别是 LLM 的发展趋势，就会发现从业人员在神经缩放定律的推动下，一直在以前所未有的水平缩放训练最近模型所需的数据量、模型大小和计算量。尽管在 2018-2022 年的时间框架内，训练这些最新模型所需的计算/浮点运算（FLOPs）增加了 750 倍/2 年（见图 2），但计算并不一定是瓶颈，尤其是在模型服务方面。

首先，在这段时间内，LLM 的规模以 410×/2 年的速度增长，超过了单芯片可用的内存。我们可能希望利用分布式内存并行性，将训练/服务扩展到多个加速器，以避免单个硬件有限的内存容量和带宽。然而，将工作分配给多个进程也会面临内存墙问题：在神经网络（NN）加速器之间移动数据的通信瓶颈，其速度和效率甚至低于片上数据移动。与单系统内存的情况类似，我们也无法克服扩展网络带宽的技术难题。

其次，即使模型适合单芯片，寄存器、二级缓存、全局存储器等的片内存储器传输仍日益成为瓶颈。得益于张量内核等专用计算单元的最新进展，大量计算的算术运算可以在几个周期内完成。因此，要让这些运算单元始终处于可用状态，就需要快速向它们提供大量数据，而这正是芯片内存带宽成为瓶颈的原因。

如图 1 所示，在过去 20 年中，服务器硬件 FLOPS 的峰值以 3.0 倍/2 年的速度增长，超过了 DRAM 和互连带宽的增长速度，而 DRAM 和互连带宽的增长速度分别仅为 1.6 倍/2 年和 1.4 倍/2 年。这种差距使得内存而非计算日益成为瓶颈，即使是在模型可以容纳在单个芯片内的情况下也是如此。

接下来，我们将对 Transformers 进行详细的案例研究，通过分析目前常用的模型，更好地展示 FLOP、内存操作（MOP）和端到端运行时间之间的相互作用。

图 1：不同世代互连和内存的带宽缩放以及峰值 FLOPS。可以看出，带宽增长非常缓慢。我们使用 R10000 系统对硬件峰值 FLOPS 进行了归一化处理，因为该系统曾用于报告 LeNet-5 的训练成本。

图 2：（a）多年来最先进（SOTA）模型参数数量的演变，以及人工智能加速器内存容量（绿点）。大型 Transformer 模型的参数数量以指数形式增长，每两年增长 410 倍，而单 GPU 内存仅以每两年 2 倍的速度增长。Transformer 模型的增长率是通过只考虑非推荐系统模型（红圈）计算得出的，而 GPU 内存的增长率是通过将相应的内存大小除以 6 得出的，这是相应容量可训练的最大模型的近似上限。(b) 针对不同的计算机视觉 (CV)、自然语言处理 (NLP) 和语音模型，以及 Transformer 模型的不同缩放比例（750×/2 年），训练 SOTA 模型所需的计算量（以 Peta FLOPs 为单位）。

案例研究

在本节中，我们首先概述了与 Transformer 推理相关的运行时特性和性能瓶颈。我们研究了 Transformer 架构的两种不同变体：编码器（encoder）架构（如 BERT ）和解码器（decoder）架构（如 GPT ），前者可并发处理所有token，后者则在每次迭代时自动递归处理并生成一个token。

A. 算术强度

衡量性能瓶颈的常用方法是计算只计算变换器编码器模型和只计算变换器解码器模型所需的 FLOP 总数。然而，单独使用这一指标可能会产生很大的误导。相反，我们需要研究相关运算的算术强度。算术强度是指从内存加载的每个字节可执行的 FLOP 次数。计算方法是将 FLOP 总数除以访问的字节总数（也称为 MOP 或内存操作）：

Arithmetic Intensity =# FLOPs/# MOPs. (1)

为了说明考虑算术深度的重要性，我们研究了 BERT-Base 和 BERT-Large ，以及 GPT-2 。前两个是编码器模型，其推理涉及矩阵-矩阵运算，后一个是解码器/自动回归模型，其推理涉及重复矩阵-向量乘法。

B. 剖析

为了分析 Transformer 工作负载在商用硬件上的瓶颈，我们在英特尔 Gold 6242 CPU 上对 Transformer 推理进行了剖析。图 3 显示了这些模型在不同序列长度下的总 FLOPs、MOPs、算术强度和最终延迟。

很明显，在每个序列长度下，GPT-2 的延迟都明显长于 BERT-Base 或 BERT-Large 的延迟，尽管 BERT-Base 和 GPT-2 的模型配置和端到端 FLOPs 基本相同（如图 3a 所示）。这是由于 GPT 的自动回归推理中固有的较高内存操作和较低算术强度的矩阵-向量操作（见图 3c）。与算术强度较低的模型相比，算术强度较高的模型能以相同甚至更多的 FLOPs 运行得更快。这清楚地表明了内存墙是如何成为解码器模型（在批量较小时）而不是计算的主要瓶颈的。

图 3：BERT-Base、BERT-Large 和 GPT-2 模型处理/生成不同序列长度（批量大小为 1）的剖析结果。(a) 总推理 FLOPs：注意到编码器模型的 FLOPs 更高；(b) 总推理内存操作 (MOPs)：注意到解码器 GPT 模型的 MOPs 多了几个数量级，这是因为它的矩阵-向量类型操作与编码器模型的矩阵-矩阵操作相比；(c) 算术强度：请注意，GPT-2 的算术强度要小几个数量级，这使得有效利用给定硬件的计算单元变得非常具有挑战性；(d) 不同模型的端到端延迟，以处理输入序列长度为 128 的 BERT-Base 模型为标准：请注意，尽管解码器模型的 FLOPs 较小，但其运行时间却是最慢的。详见 [18]。

有望打破围墙的解决方案

"任何指数都不可能永远持续下去"，即使对于大型超标量公司来说，以 410×/2 年的速度延迟指数扩展也不会长久可行。再加上计算能力和带宽能力之间的差距越来越大，很快就会使训练大型模型变得非常具有挑战性，因为成本将呈指数级增长。

为了继续创新并打破内存墙，我们需要重新思考人工智能模型的设计，这里有几个问题。

首先，目前设计人工智能模型的方法大多是临时性的，和/或涉及非常简单的缩放规则。例如，最近的大型变形模型大多只是最初的 BERT 模型中提出的几乎相同的基本架构的缩放版本。

其次，我们需要设计数据效率更高的人工智能模型训练方法。目前的 NNs 需要大量的训练数据和数十万次的迭代来学习，效率非常低。有些人可能会指出，这也与人类大脑的学习方式不同，人类大脑通常只需要为每个概念/类别提供很少的示例。

目前的优化和训练方法需要进行大量的超参数调整（如学习率、动量等），这往往需要进行数百次的试错才能找到正确的参数设置，从而成功训练出一个模型。因此，图 2 (b) 中报告的训练成本只是实际开销的下限，真正的成本通常要高得多。

最先进模型的规模过大，使得部署这些模型进行推理非常具有挑战性。这不仅限于 GPT-3 等模型。事实上，部署超标量公司使用的大型推荐系统也是一大挑战。

最后，硬件加速器的设计主要集中在提高峰值计算能力上，对改善内存约束工作负载的关注相对较少。这使得训练大型模型和探索其他模型（如图网络）变得困难，而图网络通常受带宽限制，无法有效利用当前的加速器。

所有这些问题都是机器学习中的基本问题。在此，我们将简要讨论针对上述三个问题的最新研究（包括我们自己的一些研究）。

A. 高效训练算法

训练 NN 模型的主要挑战之一是需要对超参数进行强制调整（brute-force hyperparameter tuning）。这包括寻找学习率（finding the learning rate）、退火时间表（annealing schedule）、收敛所需的迭代次数（iterations needed to converge）等。这为训练 SOTA 模型增加了开销。其中许多问题都是由用于训练的一阶 SGD 方法引起的。

虽然 SGD 变体很容易实现，但它们对超参数的调整并不稳健，而且很难调整新模型，因为对于新模型来说，正确的超参数集是未知的。解决这个问题的一个可行方法是使用二阶随机优化方法[43]。这些方法通常对超参数调整更加稳健，而且可以实现 SOTA 。

不过，目前的方法占用的内存要高出 3-4 倍。在这方面，微软的 Zero 框架是一个很有前途的研究方向，该框架展示了如何通过移除/分隔冗余优化状态变量，在相同内存容量下训练出 8 倍更大的模型。如果能解决这些高阶方法的开销问题，就能大大降低训练大型模型的总成本。

另一种有前途的方法包括减少内存占用和提高优化算法的数据局部性，但代价是执行更多的计算。数值线性代数中一个显著的例子是避免通信算法系列。优化 NN 训练内存的一个例子是再物化，即在前向传递过程中，我们只存储/检查点激活的一个子集，而不是保存所有激活。这就减少了特征图的内存占用，如图 4 所示。在需要时，可以重新计算其余的激活点。尽管这会增加计算量，但只需增加 20% 的计算量，就能将内存占用大幅减少 5 倍。这还能让从业人员在单芯片内存上训练大型模型，而不是利用分布式训练，因为分布式训练通常难以设置（主要的超级分频器公司除外），而且难以调试（对于非专业开发人员而言）。

有趣的是，传统趋势表明，新的 NN 模型架构是根据研究人员在单芯片内的访问权限而开发的，而不是使用复杂的分布式内存方法（见图 4）。当然，有很多反例来自大型超级计算公司，它们有专门的团队支持研究人员部署大型模型，但如果我们考虑整个社区，这样的例子就很有限了。事实上，即使是最近的 LLM，也经常要花费大量精力来压缩模型，使其适合在系统中使用，以便让更多的研究人员可以访问模型。

另一个重要的解决方案是设计对低精度训练具有鲁棒性的优化算法。事实上，人工智能加速器的重大突破之一就是使用半精度（FP16）算术，而不是单精度。这使得硬件计算能力提高了 10 倍以上。然而，利用当前的优化方法，在不降低精度的情况下进一步降低精度（从半精度降低到 INT8）一直是个难题。最近一个很有前途的趋势是混合使用 FP8 和 FP16（甚至最近的 FP4）。这一领域的算法创新肯定能让我们更有效地利用硬件，并能让芯片的更多区域用于改善内存（这通常被称为内存空隙惩罚）。

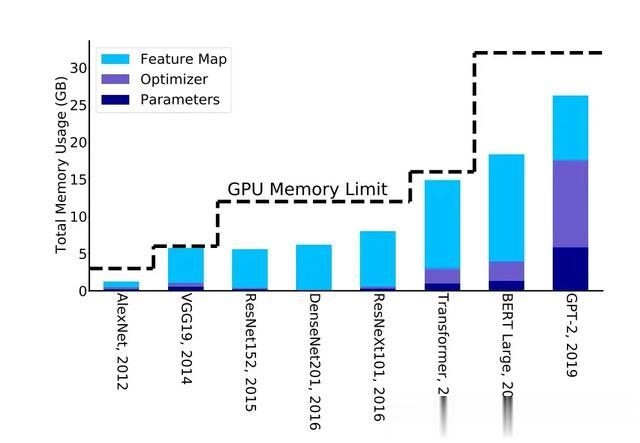
图 4：训练不同 NN 模型所需的内存量。这里，CV 模型使用的优化器是 SGD+Momentum，NLP 模型使用的优化器是 ADAM。根据 GPU 可用内存大小发现/设计新模型有一个有趣的趋势。每次 GPU 内存容量增加，数据科学家就会设计出更新的模型。因此，打破所谓的 GPU 内存墙可以进一步促进新的创新。有关检查点的更多详情，请参阅 [15]。

B. 高效部署

部署最近的 SOTA 模型如 GPT-3 [3]）或大型推荐系统相当具有挑战性，因为它们需要分布式内存部署来进行推理。解决这个问题的一个可行办法是压缩这些模型，通过降低精度（即量化）、删除（即剪枝）冗余参数或设计小语言模型来进行推理。

第一种方法，即量化，可以在训练和/或推理步骤中应用。虽然将训练精度降低到 FP16 以下非常具有挑战性，但在推理中使用超低精度是可能的。利用当前的方法，将推理量化到 INT4 精度相对容易，对精度的影响也很小。这使得模型足迹和延迟减少了 8 倍。然而，亚 INT4 精度的推理更具挑战性，目前是一个非常活跃的研究领域。

第二种方法是剪枝，即完全删除/剪除模型中的冗余参数。利用目前的方法，可以在结构稀疏的情况下剪除多达 30% 的神经元，在非结构稀疏的情况下剪除多达 80% 的神经元，而对精度的影响微乎其微。然而，突破这一限制是非常具有挑战性的，而且往往会导致致命的精度下降。解决这个问题还是一个未决难题。

第三种方法，即小语言模型，可以开辟全新的领域，使人工智能得到广泛应用。有趣的是，自 2017 年推出 Transformer 模型以来，用于 LLM 的模型一直没有改变。迄今为止，行之有效的方法是扩大模型的数据和规模，这导致了这些模型的 "新兴能力"。不过，最近关于小型语言模型的工作已在其能力方面取得了可喜的成果。如果模型能完全贴合芯片，那么就能实现数量级的提速和节能。

C. 反思人工智能加速器的设计

同时提高芯片的内存带宽和峰值计算能力面临着根本性的挑战。不过，牺牲峰值计算能力来实现更好的计算/带宽权衡是有可能的。事实上，CPU 架构已经包含了优化的高速缓存层次结构。这就是为什么在处理带宽受限问题时，CPU 的性能比 GPU 好得多。这类问题包括大型推荐问题。

然而，当今 CPU 面临的主要挑战是，其峰值计算能力（即 FLOPS）比 GPU 或 TPU 等人工智能加速器低一个数量级。其中一个原因是，人工智能加速器的设计主要是为了达到最大峰值计算能力。这通常需要移除缓存层次结构等组件，以增加更多的计算逻辑。我们可以设想一种介于这两个极端之间的替代架构，最好是采用更高效的高速缓存，更重要的是采用容量更大的 DRAM（可能是带宽不同的 DRAM 层次结构）。后者可以有效缓解分布式内存通信瓶颈。

结论

在 NLP 中，训练最新 SOTA Trans former 模型的计算成本以 750×/2yrs 的速度递增，模型参数大小以 410×/2yrs 的速度递增。相比之下，硬件 FLOPS 峰值的扩展速度为 3.0×/2yrs，而 DRAM 和互连带宽的扩展速度分别为 1.6×/2yrs 和 1.4×/2yrs，越来越落后。

从这个角度来看，硬件 FLOPS 的峰值在过去 20 年中增长了 60,000 倍，而 DRAM/互连带宽在同期仅分别增长了 100 倍/30 倍。

在这种趋势下，内存（尤其是芯片内/芯片间内存传输）将很快成为服务大型人工智能模型的主要限制因素。因此，我们需要重新思考人工智能模型的训练、部署和设计，以及如何设计人工智能硬件来应对这堵日益严峻的内存墙。

致谢本文作者：Amir Gholami，Zhewei Yao， Sehoon Kim，Coleman Hooper， Michael W. Mahoney，Kurt Keutzer，University of California, Berkeley，ICSI，LBNL

参考链接

[1] G. Ballard, J. Demmel, O. Holtz, and O. Schwartz, “Minimizing communication in numerical linear alge bra,” SIAM Journal on Matrix Analysis and Applications, vol. 32, no. 3, pp. 866–901, 2011.

[2] L. Bottou, F. E. Curtis, and J. Nocedal, “Optimization methods for large-scale machine learning,” SIAM Review, vol. 60, no. 2, pp. 223–311, 2018.

[3] T. Brown, B. Mann, N. Ryder, M. Subbiah, J. D. Ka plan, P. Dhariwal, A. Neelakantan, P. Shyam, G. Sastry, A. Askell et al., “Language models are few-shot learn ers,” Advances in neural information processing systems, vol. 33, pp. 1877–1901, 2020.

[4] A. Chowdhery, S. Narang, J. Devlin, M. Bosma, G. Mishra, A. Roberts, P. Barham, H. W. Chung, C. Sutton, S. Gehrmann et al., “Palm: Scaling language modeling with pathways,” Journal of Machine Learning Research, vol. 24, no. 240, pp. 1–113, 2023.

[5] H. W. Chung, L. Hou, S. Longpre, B. Zoph, Y. Tay, W. Fedus, Y. Li, X. Wang, M. Dehghani, S. Brahma et al.,

“Scaling instruction-finetuned language models,” arXiv preprint arXiv:2210.11416, 2022.

[6] T. Dettmers, R. Svirschevski, V. Egiazarian, D. Kuznedelev, E. Frantar, S. Ashkboos, A. Borzunov, T. Hoefler, and D. Alistarh, “Spqr: A sparse-quantized representation for near-lossless llm weight compression,” arXiv preprint arXiv:2306.03078, 2023.

[7] J. Devlin, M.-W. Chang, K. Lee, and K. Toutanova, “BERT: Pre-training of deep bidirectional transformers for language understanding,” in Proceedings of the 2019 Conference of the North American Chapter of the Asso ciation for Computational Linguistics: Human Language Technologies, Volume 1 (Long and Short Papers), 2019, pp. 4171–4186.

[8] E. Frantar and D. Alistarh, “Sparsegpt: Massive language models can be accurately pruned in one-shot,” 2023.

[9] E. Frantar, S. Ashkboos, T. Hoefler, and D. Alistarh,

“OPTQ: Accurate quantization for generative pre-trained transformers,” in The Eleventh International Conference on Learning Representations, 2023.

[10] A. Gholami, S. Kim, Z. Dong, Z. Yao, M. W. Mahoney, and K. Keutzer, “A survey of quantization methods for efficient neural network inference,” in Low-Power Computer Vision. Chapman and Hall/CRC, 2022, pp. 291–326.

[11] B. Ginsburg, S. Nikolaev, A. Kiswani, H. Wu, A. Gho laminejad, S. Kierat, M. Houston, and A. Fit-Florea, “Tensor processing using low precision format,” Dec. 28 2017, uS Patent App. 15/624,577.

[12] J. L. Hennessy and D. A. Patterson, Computer architec ture: a quantitative approach. Elsevier, 2011.

[13] T. Hoefler, D. Alistarh, T. Ben-Nun, N. Dryden, and A. Peste, “Sparsity in deep learning: Pruning and growth for efficient inference and training in neural networks,” The Journal of Machine Learning Research, vol. 22, no. 1, pp. 10 882–11 005, 2021.

[14] J. Hoffmann, S. Borgeaud, A. Mensch, E. Buchatskaya, T. Cai, E. Rutherford, D. de Las Casas, L. A. Hendricks, J. Welbl, A. Clark, T. Hennigan, E. Noland, K. Millican, G. van den Driessche, B. Damoc, A. Guy, S. Osin dero, K. Simonyan, E. Elsen, O. Vinyals, J. Rae, and L. Sifre, “An empirical analysis of compute-optimal large language model training,” in Advances in Neural Infor mation Processing Systems, vol. 35, 2022, pp. 30 016– 30 030.

[15] P. Jain, A. Jain, A. Nrusimha, A. Gholami, P. Abbeel, J. Gonzalez, K. Keutzer, and I. Stoica, “Checkmate: Breaking the memory wall with optimal tensor remate rialization,” Proceedings of Machine Learning and Sys tems, vol. 2, pp. 497–511, 2020.

[16] A. Q. Jiang, A. Sablayrolles, A. Mensch, C. Bamford, D. S. Chaplot, D. d. l. Casas, F. Bressand, G. Lengyel, G. Lample, L. Saulnier et al., “Mistral 7b,” arXiv preprint arXiv:2310.06825, 2023.

[17] S. Kim, C. Hooper, A. Gholami, Z. Dong, X. Li, S. Shen, M. W. Mahoney, and K. Keutzer, “Squeezellm: Dense-and-sparse quantization,” arXiv preprint arXiv:2306.07629, 2023.

[18] S. Kim, C. Hooper, T. Wattanawong, M. Kang, R. Yan, H. Genc, G. Dinh, Q. Huang, K. Keutzer, M. W. Ma honey, Y. S. Shao, and A. Gholami, “Full stack optimiza tion of transformer inference: a survey,” Workshop on Architecture and System Support for Transformer Models (ASSYST) at ISCA, 2023.

[19] V. A. Korthikanti, J. Casper, S. Lym, L. McAfee, M. Andersch, M. Shoeybi, and B. Catanzaro, “Reducing activation recomputation in large transformer models,” Proceedings of Machine Learning and Systems, vol. 5, 2023.

[20] S. Krishna and R. Krishna, “Accelerating recom mender systems via hardware scale-in,” arXiv preprint arXiv:2009.05230, 2020.

[21] W. Kwon, S. Kim, M. W. Mahoney, J. Hassoun, K. Keutzer, and A. Gholami, “A fast post-training prun ing framework for transformers,” in Advances in Neural Information Processing Systems, vol. 35. Curran Asso ciates, Inc., 2022, pp. 24 101–24 116.

[22] Y. LeCun, L. Bottou, Y. Bengio, P. Haffner et al., “Gradient-based learning applied to document recogni tion,” Proceedings of the IEEE, vol. 86, no. 11, pp. 2278– 2324, 1998.

[23] J. Lin, J. Tang, H. Tang, S. Yang, X. Dang, C. Gan, and S. Han, “Awq: Activation-aware weight quantization for llm compression and acceleration,” 2023.

[24] J. McCalpin, “Stream: Sustainable memory bandwidth in high performance computers,” http://www. cs. virginia. edu/stream/, 2006.

[25] S. A. McKee, “Reflections on the memory wall,” in Pro ceedings of the 1st Conference on Computing Frontiers, ser. CF ’04. New York, NY, USA: Association for Computing Machinery, 2004, p. 162.

[26] P. Micikevicius, S. Narang, J. Alben, G. Diamos, E. Elsen, D. Garcia, B. Ginsburg, M. Houston, O. Kuchaiev, G. Venkatesh, and H. Wu, “Mixed preci sion training,” in International Conference on Learning Representations, 2018.

[27] P. Micikevicius, D. Stosic, N. Burgess, M. Cornea, P. Dubey, R. Grisenthwaite, S. Ha, A. Heinecke, P. Judd, J. Kamalu et al., “Fp8 formats for deep learning,” arXiv preprint arXiv:2209.05433, 2022.

[28] G. Moore, “No exponential is forever: but ”forever” can be delayed! [semiconductor industry],” in 2003 IEEE In ternational Solid-State Circuits Conference, 2003. Digest of Technical Papers. ISSCC., 2003, pp. 20–23 vol.1.

[29] M. Naumov, D. Mudigere, H.-J. M. Shi, J. Huang, N. Sundaraman, J. Park, X. Wang, U. Gupta, C.-J. Wu, A. G. Azzolini et al., “Deep learning recommendation model for personalization and recommendation systems,” arXiv preprint arXiv:1906.00091, 2019.

[30] J. Ousterhout, “Why aren’t operating systems getting faster as fast as hardware?” in USENIX Summer Con ference, 1990, 1990.

[31] D. Patterson, T. Anderson, N. Cardwell, R. Fromm, K. Keeton, C. Kozyrakis, R. Thomas, and K. Yelick, “A case for intelligent ram,” IEEE micro, vol. 17, no. 2, pp. 34–44, 1997.

[32] D. A. Patterson, “Latency lags bandwith,” Communica tions of the ACM, vol. 47, no. 10, pp. 71–75, 2004.

[33] A. Radford, J. Wu, R. Child, D. Luan, D. Amodei,

and I. Sutskever, “Language models are unsupervised multitask learners,” OpenAI blog, vol. 1, no. 8, p. 9, 2019.

[34] S. Rajbhandari, J. Rasley, O. Ruwase, and Y. He, “Zero: Memory optimizations toward training trillion parameter models,” in SC20: International Conference for High Performance Computing, Networking, Storage and Anal ysis. IEEE, 2020, pp. 1–16.

[35] T. Schick and H. Schutze, “It’s not just size that matters: ¨ Small language models are also few-shot learners,” arXiv preprint arXiv:2009.07118, 2020.

[36] D. Sites, “It’s the memory, stupid!” Microprocessor Re port, pp. 18–24, 1996.

[37] H. Touvron, L. Martin, K. Stone, P. Albert, A. Almahairi, Y. Babaei, N. Bashlykov, S. Batra, P. Bhargava, S. Bhos ale et al., “Llama 2: Open foundation and fine-tuned chat models,” arXiv preprint arXiv:2307.09288, 2023.

[38] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, and I. Polosukhin, “Attention is all you need,” in Advances in neural infor mation processing systems, 2017, pp. 5998–6008.

[39] J. Wei, Y. Tay, R. Bommasani, C. Raffel, B. Zoph, S. Borgeaud, D. Yogatama, M. Bosma, D. Zhou, D. Met zler et al., “Emergent abilities of large language models,” arXiv preprint arXiv:2206.07682, 2022.

[40] M. V. Wilkes, “The memory wall and the cmos end point,” ACM SIGARCH Computer Architecture News, vol. 23, no. 4, pp. 4–6, 1995.

[41] S. Williams, A. Waterman, and D. Patterson, “Roofline: an insightful visual performance model for multicore architectures,” Communications of the ACM, vol. 52, no. 4, pp. 65–76, 2009.

[42] W. A. Wulf and S. A. McKee, “Hitting the memory wall: Implications of the obvious,” ACM SIGARCH computer architecture news, vol. 23, no. 1, pp. 20–24, 1995.

[43] Z. Yao, A. Gholami, S. Shen, M. Mustafa, K. Keutzer, and M. Mahoney, “Adahessian: An adaptive second order optimizer for machine learning,” in proceedings of the AAAI conference on artificial intelligence, vol. 35, no. 12, 2021, pp. 10 665–10 673.

[44] Z. Yao, R. Yazdani Aminabadi, M. Zhang, X. Wu, C. Li, and Y. He, “Zeroquant: Efficient and affordable post-training quantization for large-scale transformers,” in Advances in Neural Information Processing Systems, S. Koyejo, S. Mohamed, A. Agarwal, D. Belgrave, K. Cho, and A. Oh, Eds., vol. 35. Curran Associates, Inc., 2022, pp. 27 168–27 183.