“全军覆没,几乎集体白卷!”不少家长也束手无策、望题兴叹!这是一道五年级数学同步训练拓展题:如图一,

图一
仅用一副三角板,如何作一面积为2cm²的正方形?
难点:①面积为2cm²正方形的边长无法求出。②即便能求出(实际为√2,需使用勾股定理及带根号的无理数),若以其边长为作图依据,也只能作近似图、无法作精确图。
作法一:
①作一边长为2cm大正方形,其面积为4cm²。
②连接正方形的各边中点,即得一小正方形,其面积为大正方形面积的一半即2cm²,如图二

图二
作法二:
①作图依据:作一边长为2cm、面积为4cm²的大正方形。连接两对角线,大正方形被将四等分为4个面积为1cm²的等腰直角三角形。如图三

图三
②在三角形AOB、BOC、COD和AOD中,任取两个并将其斜边对齐即得一面积为2cm²的小正方形。
或②'在三角形AOB、BOC、COD和AOD中,任选两个相邻的两个并将其中一个旋转90°即得一面积为2cm²的小正方形。
注:作法二理论上成立,但在具体作图中可操作性极差!
为此,在作法二依据的基础上,给出如下作法:
作法三:
①画一长2cm的线段AB。
②以其为斜边,在其两侧各作一个等腰直角三角形ABC和ABD,由作法二的依据可知,这两个等腰直角三角形的面积均为1cm²。
③将两个直角三角形视为一个整体图形,即得一面积为2cm²的正方形ACBD。如图四
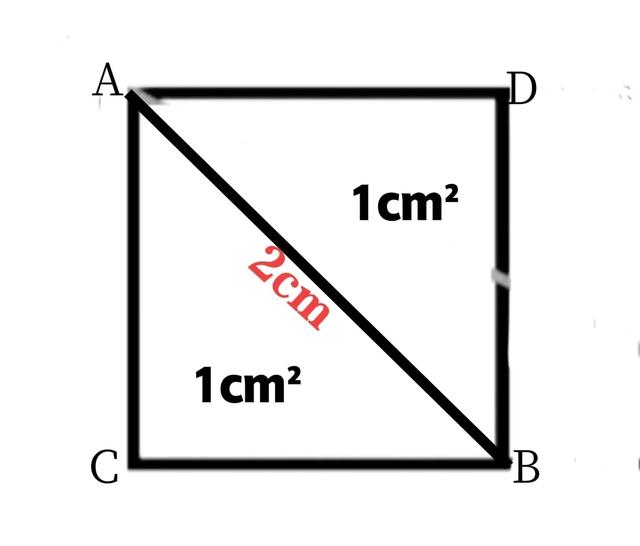
图四
———————————————————————
友友们有啥想法或思路,欢迎留言分享!
