猎鹿博弈又称猎鹿模型，源自启蒙思想家卢梭的著作《论人类不平等的起源和基础》中的一个故事：

古代的村庄有两个猎人。当地的猎物主要有两种：鹿和兔子。如果一个猎人单兵作战，一天最多只能打到4只兔子。只有两个一起去才能猎获一只鹿。从填饱肚子的角度来说，4只兔子能保证一个人4天不挨 饿，而一只鹿却能让两个人吃上10天。这样两个人的行为决策可以形成两个博弈结局：分别打兔子，每人得4；合作，每人得10。这样猎鹿博弈有两个纳什均衡点，那就是：要么分别打兔子，每人吃饱4天；要么合作，每人吃饱10天。

显然，两个人合作猎鹿的好处比各自打兔子的好处要大得多，但是要求两个猎人的能力和贡献相等。如果一个猎人的能力强、贡献大，他就会要求得到较大的一份，这可能会让另一个猎人觉得利益受损而不愿意合作。合则双赢的道理大家都懂，在实际中很难合作的原因就在于 此。合作要求博弈双方学会与对手共赢，充分照顾到合作者的利益。

诺斯悖论是诺斯在1981年提出，国家具有双重目标，一方面通过向不同的势力集团提供不同的产权，获取租金的最大化；另一方面，国家还试图降低交易费用以推动社会产出的最大化，从而获取国家税收的增加。国家的这两个目标经常是冲突的。另外，由于存在着投票悖论、理性的无知，加之政治市场的竞争更不充分和交易的对象更难以考核等因素，政治市场的交易费用高昂。结果，政府作用的结果往往是经济增长的停滞。

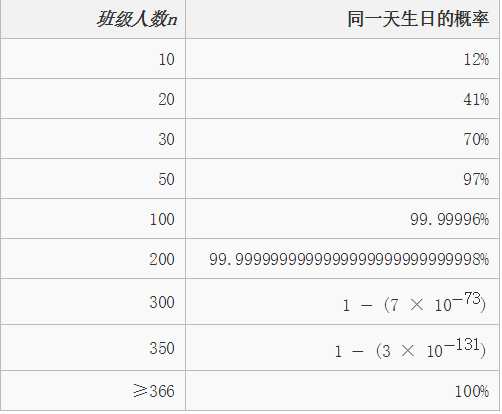
生日悖论（Birthday Paradox）是指，如果一个房间里有23个或23个以上的人，那么至少有两个人的生日相同的概率要大于50％。这就意味着在一个典型的标准小学班级（30人）中，存在两人生日相同的可能性更高。对于60或者更多的人，这种概率要大于99％。从引起逻辑矛盾的角度来说生日悖论并不是一种悖论，从这个数学事实与一般直觉相抵触的意义上，它才称得上是一个悖论。大多数人会认为，23人中有2人生日相同的概率应该远远小于50％。计算与此相关的概率被称为生日问题，在这个问题之后的数学理论已被用于设计著名的密码攻击方法：生日攻击。