在信息论、机器学习和统计学领域中，KL散度（Kullback-Leibler散度）作为一个基础概念，在量化概率分布差异方面发挥着关键作用。它常用于衡量当一个概率分布用于近似另一个概率分布时的信息损失。本文将深入探讨KL散度及其他相关的重要散度概念。

KL散度，也称为相对熵，是衡量两个概率分布P和Q之间差异的有效方法。其数学表达式如下：

离散分布P(x)和Q(x)之间的KL散度

连续分布P(x)和Q(x)之间的KL散度

这些方程比较了真实分布P与近似分布Q。在实际应用中可以将KL散度理解为：当使用为分布Q优化的编码系统来压缩来自分布P的数据时，所产生的额外编码成本。如果Q与P相近，KL散度值较小，表示信息损失较少；反之，如果Q与P差异显著，KL散度值较大，意味着信息损失更多。换言之，KL散度量化了使用为Q设计的编码方案来编码P分布数据时所需的额外比特数。

为深入理解KL散度，将其与熵的概念联系起来至关重要。熵是衡量分布不确定性或随机性的指标。香农熵的定义如下：

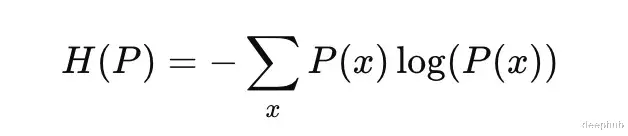
分布P(x)的香农熵

熵是不确定性的度量，其值越低，表示对结果的确定性越高，即拥有的信息量越大。在二元情况下，当概率p=0.5时，熵达到最大值，这代表了最大的不确定性。

香农熵图（对数以e为底，也可取2为底）

KL散度可以被视为P的熵与P和Q之间"交叉熵"的差值。因此KL散度实际上衡量了使用Q而非P所引入的额外不确定性。

从熵推导KL散度

非负性：KL散度始终大于等于零。

非负性证明

不对称性：与许多距离度量不同，KL散度是不对称的。

KL散度的不对称性

变分自编码器（VAE）：在VAE中，KL散度作为正则化器，确保潜在变量分布接近先验分布（通常是标准高斯分布）。

数据压缩：KL散度量化了使用一个概率分布压缩来自另一个分布的数据时的效率损失，这在设计和分析数据压缩算法时极为有用。

强化学习：在强化学习中，如近端策略优化（PPO）算法，KL散度用于控制新策略与旧策略之间的偏离程度。

数据漂移检测：在工业应用中，KL散度广泛用于检测数据分布随时间的变化。

Jensen-Shannon散度（JS散度）是一种对称的散度度量，用于量化两个概率分布间的相似性。它基于KL散度构建，但克服了KL散度不对称的局限性。给定两个概率分布P和Q，JS散度定义如下：

Jensen-Shannon散度

其中M是P和Q的平均（或混合）分布：

混合分布

JS散度的第一项衡量当M用于近似P时的信息损失，第二项则衡量M近似Q时的信息损失。通过计算相对于平均分布M的两个KL散度的平均值，JS散度提供了一种更均衡的分布比较方法。

这种方法解决了KL散度在分布比较中的不对称性问题。JS散度不将P或Q视为"标准"分布，而是通过混合分布M来评估它们的综合行为。这使得JS散度在需要无偏比较分布的场景中特别有用。

Renyi熵是香农熵的广义形式，为我们提供了一种更灵活的方式来衡量分布的不确定性。分布的Renyi熵定义为：

分布P(x)的Renyi熵，参数为α

Renyi熵由参数α > 0控制，该参数决定了对分布中不同概率的权重分配。

当α = 1时，Renyi熵等同于香农熵，对所有可能事件给予相等权重。这可以通过极限和洛必达法则证明：

从Renyi熵推导香农熵

当α < 1时，熵计算对低概率事件（稀有事件）更敏感，更侧重于分布的多样性或分散性。

当α > 1时，熵计算对高概率事件更敏感，更关注分布的集中度或主导事件。

不同α值的Renyi熵图（对数以e为底，也可取2为底）

当α = 0时，Renyi熵趋近于可能结果数量的对数（假设所有结果概率非零），这被称为Hartley熵。

当α → ∞时，Renyi熵变为最小熵，仅关注最可能发生的结果：

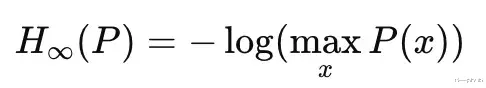
最小熵

基于Renyi熵，我们可以定义Renyi散度，它是KL散度的推广。两个分布P和Q之间的Renyi散度，参数化为α，定义如下：

两个离散分布P(x)和Q(x)之间的Renyi散度，参数为α

KL散度是Renyi散度在α = 1时的特例：

从Renyi散度推导KL散度

Renyi散度的特性随α值变化：

当α < 1时，散度计算更关注稀有事件，对分布尾部更敏感。

当α > 1时，散度计算更侧重于常见事件，对高概率区域更敏感。

P和Q之间的Renyi散度图。

Renyi散度始终非负，当且仅当P = Q时等于0。上图展示了当改变分布P时散度的变化情况。散度随α值的增加而增加，较高的α值使Renyi散度对概率分布的变化更为敏感。

Renyi散度在差分隐私（Differential Privacy）领域找到了重要应用，这是隐私保护机器学习中的一个关键概念。差分隐私提供了一个数学框架，用于保证个体数据在数据集中的隐私性。它确保算法输出不会因单个数据点的存在或缺失而发生显著变化。

Renyi差分隐私（RDP）是差分隐私的一个扩展，利用Renyi散度提供更精确的隐私保证。这一方法在需要更细粒度隐私控制的场景中特别有用。

在电子商务领域，用户行为的潜在概率分布可能随时间发生变化，导致数据漂移。这种漂移可能影响诸如产品推荐等多个业务方面。下面我们将通过一个简化的示例展示如何利用不同的散度指标来检测这种漂移。

考虑一个电子商务平台，该平台跟踪客户在五个产品类别中的购买行为：电子产品、服装、图书、家居与厨房、以及玩具。该平台每周收集各类别的点击比例数据，以概率分布的形式表示。以下是连续七周的数据：

weeks = {      'Week 1': np.array([0.3, 0.4, 0.2, 0.05, 0.05]),      'Week 2': np.array([0.25, 0.45, 0.2, 0.05, 0.05]),      'Week 3': np.array([0.2, 0.5, 0.2, 0.05, 0.05]),      'Week 4': np.array([0.15, 0.55, 0.2, 0.05, 0.05]),      'Week 5': np.array([0.1, 0.6, 0.2, 0.05, 0.05]),      'Week 6': np.array([0.1, 0.55, 0.25, 0.05, 0.05]),      'Week 7': np.array([0.05, 0.65, 0.25, 0.025, 0.025]),  }

数据分析显示以下趋势：

第1周至第2周：观察到轻微漂移，第二类别（服装）的点击比例略有增加。

第3周：出现更明显的漂移，服装类别的主导地位进一步增强。

第5周至第7周：发生显著变化，服装类别持续增加其点击份额，而其他类别，尤其是电子产品类别，相对重要性下降。

为量化这些变化，我们可以实现以下散度计算函数：

# KL散度计算def kl_divergence(p, q):      return np.sum(kl_div(p, q))  # Jensen-Shannon散度计算def js_divergence(p, q):      m = 0.5 * (p + q)      return 0.5 * (kl_divergence(p, m) + kl_divergence(q, m))  # Renyi散度计算def renyi_divergence(p, q, alpha):      return (1 / (alpha - 1)) * np.log(np.sum(np.power(p, alpha) * np.power(q, 1 - alpha)))

利用这些函数可以计算并绘制不同散度随时间的变化：

随时间变化的散度测量

KL散度：随时间呈现上升趋势，表明购买分布逐渐偏离初始基准。从第1周到第7周，KL散度的增加突显了第二类别（服装）持续增长的主导地位。

Jensen-Shannon散度：展现出类似的平稳上升趋势，进一步确认了分布的逐步变化。JS散度捕捉到了各类别的整体漂移情况。

Renyi散度：根据所选α值呈现不同的变化模式：

α = 0.5时：散度对稀有类别（如家居与厨房、玩具）更为敏感。它在这些类别出现波动时（特别是第6周到第7周，当它们的概率降至0.025）能更早地捕捉到漂移。

α = 2时：散度突出显示了服装类别的持续增长，反映出高概率事件的变化，表明分布正变得更加集中。

通过持续监测这些散度指标，电子商务平台可以：

及时检测用户行为模式的变化。

根据检测到的漂移调整业务策略，如重新训练推荐系统。

深入分析导致漂移的潜在因素，如季节性趋势或营销活动的影响。

这个实例展示了如何将理论概念应用于实际业务场景，突显了不同散度指标在捕捉数据分布变化方面的独特优势。通过综合运用这些工具，企业可以更精准地把握市场动态，做出数据驱动的决策。

本文深入探讨了信息论、机器学习和统计学中的几个核心概念：熵、KL散度、Jensen-Shannon散度和Renyi散度。这些概念不仅是理论研究的基石，也是现代数据分析和机器学习应用的重要工具。

熵作为信息论的基础，为我们量化信息和不确定性提供了数学框架。而各种散度度量则进一步扩展了这一概念，使我们能够比较和分析不同的概率分布。KL散度凭借其在衡量分布差异方面的独特性质，在诸如变分推断、模型压缩等领域发挥着关键作用。Jensen-Shannon散度通过其对称性质，为我们提供了一种更均衡的分布比较方法，特别适用于需要无偏比较的场景。Renyi散度则通过其可调参数α，为我们提供了一系列灵活的散度度量，能够根据具体需求关注分布的不同方面。

这些理论概念在实际应用中的价值不容忽视。正如我们在电子商务数据漂移检测的案例中所看到的，这些散度指标能够有效地捕捉数据分布随时间的变化。这不仅限于电子商务，在金融风险评估、生物信息学、自然语言处理等众多领域，这些概念都有着广泛的应用。

随着大数据时代的深入发展和人工智能技术的不断进步，对数据分布的精确分析和比较变得越来越重要。熵和各种散度指标为我们提供了强大的工具，使我们能够从海量数据中提取有价值的信息，识别潜在的模式和趋势，并做出数据驱动的决策。

展望未来，这些概念很可能会在更多新兴领域找到应用，如量子计算中的信息处理、复杂网络分析等。同时，研究者们也在不断探索这些概念的新变体和扩展，以应对increasingly复杂的数据分析挑战。

总之，熵、KL散度、JS散度和Renyi散度不仅是理论研究的重要主题，更是连接抽象数学概念与实际数据分析的桥梁。掌握这些工具，将使我们能够更深入地理解和分析复杂的数据世界，为科学研究和技术创新提供强大支持。

https://avoid.overfit.cn/post/a9500fa46ac34f318444c4e566a558dd

作者：Saankhya Mondal