目录大纲
资产收益率简单收益率连续复利收益率现值分析资产组合收益率红利支付与收益率超额收益率正文部分
资产收益率设为某资产在时刻的价格或净值,按照某种时间单位(如年)计数。
1. 简单收益率单期简单毛收益率:
单期简单净收益率(简单收益率):
期简单毛收益率:
期净收益率:
在实际中, 收益率(利率)一般按年为单位, 但是计息区间长度可以不等于一年。
在实际中, 收益率(利率)一般按年为单位, 但是计息区间长度可以不等于一年。
【例】设在银行借款金额为,名义年利率为,以半年计息一次的复利方式计算利息, 一年后偿还本金和利息。如何计算本息?
【解】年名义利率为,若每年计息次,则年的简单收益率为。因此,当半年计息一次时,半年期的利率为。
半年后的本息合计为,利息合并进入本金(复利方式),后半年的本息合计为。因此,1年后需要偿还的本息为。
相应地,我们可以计算出实际利率(有效利率),由
可得
是以1年为时间单位的简单收益率。
更进一步地,如果名义利率为,分期计息,则实际利率为
当某资产持有年时,按复利计算的平均年化收益率为
即
当各都很小时,根据,可近似地将期平均年化复利写为
2. 连续复利收益率设某资产的初始值为,名义年利率为,但是一年内分成次付息,每次付息,提前支付的利息也将进入账户增值,一年后的价值将高于,确切而言,一年后的价值为:
当时,上式极限为,此时称为连续复利,连续复利对应的实际利率应为
即有。
因此,若按照连续复利计算,设初始资产价格为,名义年利率为,则年后的资产价值为:
当时,
其中,为简单收益率,可以被称为连续复合收益率或对数收益率。
对多期连续复合收益率,有
3. 现值分析假设可以以每期计息一次的方式,以每期的名义利率借款和贷款。这时,第期的期末支付元的当前价值是多少?应为使得
即。
考虑一项投资,初始支出为,随后每期分别得到回报。定义该投资每期的回报率为下述利率的值:使得在该利率下现金流序列的复利现值等于零,即
4. 资产组合收益率设有项资产,在时刻组合价值为
其中,为第项资产的权重。
于是,
因此,资产组合的简单收益率为:
注意,其中的是第时刻的权重。当然,如果资产比例变化不大,使用不变的近似也是可以的。
5. 红利支付与收益率对价格的某资产,如果在到之间每单位还支付红利,则到时刻时,收益为,所以此时收益率应计算为
6. 超额收益率考虑
超额收益率被认为是如下的套利投资组合的盈利:对该资产持有多头头寸,对参照资产持有空头头寸,且初始净投资额为零。
多头金融头寸是指持有某资产。空头头寸是指从持有某资产的投资者手里借入某资产,然后卖出这些不属于自己的资产,在随后的规定日期卖空者有义务通过买入相同数额的该资产偿还借出者,不能偿还现金,当规定日期时该资产价格下跌时空头持有者可以获利。
最后我们来做一个简单的小结。
简单收益率与连续复合收益率(对数收益率)的关系为:
简单的期收益率为:
期对数收益率为:
如果连续复合年利率固定为,初始资产价值为,年后资产价值为,则
https://mp.weixin.qq.com/s?__biz=MzkzOTQwMTM5MA==&mid=2247483709&idx=1&sn=c4c64a9ce9b6bcbb9277504124ada9b5&chksm=c2f0c8fcf58741eaa6dbc544cee245b29fbe0e53bb771fad4a3d9c287abdf1ecf09e5d32fc4d&cur_album_id=2557243622212141057&scene=189#wechat_redirect
金融数据及其特征(2)目录大纲
债券收益和价格债券类型当期收益率到期收益率收益率的分布特性苹果公司股票日数据美国十年期国债日数据欧元对美元汇率日数据正文部分
1. 债券收益和价格
1.1. 债券类型投资者以低于票面价格的市场价格买入债券,并在到期日收回票面价格的现金。
有些债券还在持有期间定期派发利息,利息按照票面利率(coupon payment)和面额计算,比如,面值为100元,票面利率为6%,如果每半年派发一次利息,则每次派息100×6%/2=3元。有些债券不在持有期间派息,这样的债券称为零息债券。
1.2. 当期收益率当期收益率仅计算每年的表面收益,而不考虑资金的时间成本。其计算公式如下:
当期收益率每年派息额买入价格
比如,票面价格100元,买入价格90元,票面利率为每年5%,则持有一年的当期收益率为
但是,当期收益率没有考虑到在到期时票面价格与买入价格差值造成的收益。
1.3. 到期收益率首先我们来看不派息的零息债券。假设其购入价格为,面值为, 持有年到期,则到期收益率(Yield To Maturity, YTM)为
但是,如果持有债券期间存在派息,那么此时到期收益率的计算就更为复杂一些。当期收益率是使得未来支付的现值等于当前债券的价格的利率。
设投资者购买债券时的价格为,债券的面额为,共派息次,每次派息额为。到期收益率为。
当每年派一次息时就是年化的到期收益率。
若票面利率(名义年利率)为,投资者持有年,每年派息次,则。每次派息。设按照年计算的到期收益率为,则到期收益率满足的方程为
实际年化利率为。
我们来看一个例子。
【例】设某债券面值为元,售价为,持有时间为年,每年发息次,票面利率为, 则一共有次发息,每次发息元。设到期收益率按半年期利率计算为,则售价与到期收益率(半年期)之间的关系为
我们可以作对的曲线图(使用R语言),
# 定义函数f<-function(y){ (2.5/y)*(1-(1+y)^{-6})+100*(1+y)^{-6}}# 绘制P对y的曲线curve(f(x),0.028,0.052,xlab = "半年期到期收益率",ylab = "售价")# 绘制网格abline(v=c(0.030, 0.035, 0.040, 0.045, 0.050), col="gray")abline(h=c(97.29, 94.67, 92.14, 89.68, 87.31), col="gray")
图1
图中画出了半年期到期利率为3%,3.5%,4%,4.5%,5%时的售价。如果半年期到期利率为3%,售价为97.29元。半年期到期利率3%转换为年化到期利率,结果为。
2. 收益率的分布特性
在介绍收益率的分布特性前,我们简要说明一下几个概念。
偏度(Skewness):令称为的标准化,的三阶矩称为的偏度。偏度可以用来度量分布的对称性,负偏度称为左偏,反映左尾偏长的情况;正偏度称为右偏,反映右尾偏长的情况。
峰度(Kurtosis):将标准化为,的四阶矩减去3称为的超额峰度或峰度,正态分布的超额峰度等于0。峰度大的分布有重尾或厚尾现象,其分布密度在处趋于零速度较慢,其样本具有较多的异常值(离群值,outliers)。
如果样本为独立的正态分布样本,则充分大时样本偏度渐近服从分布,样本超额峰度渐近服从分布,
Jarque-Bera检验的零假设:总体服从正态分布。
下面我们来看三个例子。并且,我们将在最后对苹果公司股票日数据进行更为详细的分析。
quantmod软件包下载数据似乎会遇到很多问题。笔者暂时无法通过quantmod下载数据。笔者目前找到的解决方式是:在https://rstudio.cloud这一网址注册,相同的代码可以在此网页版的R studio中运行,但是无法在电脑上安装的R studio中运行。在此,感谢作者https://blog.csdn.net/Mrrunsen/article/details/125818596提供的解决方案。
2.1 苹果公司股票日数据苹果公司日数据下载:
# 下载包install.packages("quantmod")# 载入包library(quantmod)# 从雅虎财经中获取苹果公司股票数据(时间为2007-01-03/2022-09-21)AAPL <- getSymbols("AAPL", src="yahoo", auto.assign=FALSE)计算对数收益率:
# 计算对数收益率(注意,要使用调整后的收盘价)logret.AAPL <- diff(log(AAPL$AAPL.Adjusted))*100logret.AAPL<-na.omit(logret.AAPL)绘制对数收益率时间序列2007-2022的曲线图:
# 绘制对数收益率时间序列2007-2022的曲线图chartSeries(logret.AAPL,type = "l",name = "Apple Log Returns",TA=NULL, theme = chartTheme("white"),major.ticks="years",minor.ticks=FALSE)
图2
仅绘制2021年的对数收益率曲线图:
# 仅绘制2021年的对数收益率曲线图chartSeries(logret.AAPL,type = "l",name = "Apple Log Returns",TA=NULL, subset="2021/2021",theme = chartTheme("white"),major.ticks="months",minor.ticks=FALSE)
图3
对数收益率的直方图:
# 对数收益率的直方图x<-coredata(logret.AAPL)hist(x,main = "Apple Log Returns",xlab = " ",ylab = " ")
图4
对数收益率的QQ图:
# 对数收益率的QQ图qqnorm(x,main = "Apple Log Returns")qqline(x,col="red")
图5
显然,苹果股票的对数收益率存在厚尾现象。
2.2 美国十年期国债日数据美国十年期国债日数据下载:
# 从雅虎财经中获取美国十年期国债日数据(时间为2007-01-03/2022-09-21)TNX<-getSymbols("^TNX",src = "yahoo",auto.assign = FALSE) # 股指等的symbol需要加^TNX<-na.omit(TNX) # 去除缺失值计算对数收益率:
# 计算对数收益率(注意,要使用调整后的数据)logret.TNX <- diff(log(TNX$TNX.Adjusted))*100 logret.TNX <- na.omit(logret.TNX)绘制对数收益率时间序列2007-2022的曲线图:
# 绘制对数收益率时间序列2007-2022的曲线图chartSeries(logret.TNX,type = "l",name = "US 10 Years T Notes Log Return",TA=NULL, theme = chartTheme("white"),major.ticks="years",minor.ticks=FALSE)
图6
对数收益率的直方图:
# 对数收益率的直方图x<-coredata(logret.TNX)hist(x,nclass = 40,main = "US 10 Year T Notes Log Returns",xlab = " ",ylab = " ")
图7
对数收益率的QQ图:
qqnorm(x,main = "US 10 Year T Notes Log Returns")qqline(x,col="red")
图8
美国十年期国债的对数收益率同样存在厚尾现象。
2.3 欧元对美元汇率日数据下载欧元对美元汇率的日数据,为一元时间序列:
# 从美联储经济数据中获取欧元对美元汇率日数据(时间为1999-01-04/2022-09-16)DEXUSEU <- getSymbols("DEXUSEU", src="FRED", auto.assign=FALSE) # 一元时间序列DEXUSEU<-na.omit(DEXUSEU)计算对数收益率:
# 计算对数收益率logret.DEXUSEU <- diff(log(DEXUSEU))*100logret.DEXUSEU <- na.omit(logret.DEXUSEU)汇率价格的曲线图:
# 汇率价格的曲线图chartSeries(DEXUSEU,type = "l",TA=NULL,name = "Euro to USD Price", theme = chartTheme("white"),major.ticks = "years",minor.ticks = FALSE)
图9
绘制对数收益率时间序列1999-2022的曲线图:
# 绘制对数收益率时间序列1999-2022的曲线图chartSeries(logret.DEXUSEU,type = "l",TA=NULL,name = "Euro to USD Log Returns", theme = chartTheme("white"),major.ticks = "years",minor.ticks = FALSE)
图10
对数收益率的直方图:
# 对数收益率的直方图x<-coredata(logret.DEXUSEU)hist(x,nclass = 30,main = "Euro to USD Log Returns",xlab = " ",ylab = " ")
图11
对数收益率的QQ图:
# 对数收益率的QQ图qqnorm(x,main = "Euro to USD Log Returns")qqline(x,col="red")
图12
欧元对美元汇率的对数收益率同样存在厚尾现象。
最后,我们对苹果公司股票日数据进行更为详细的分析。
苹果公司股票日收盘价的对数收益率的描述性统计分析:
# 对苹果公司股票日数据的进一步分析library(fBasics)x<-coredata(logret.AAPL)colnames(x)<-"x"basicStats(x)# x# nobs 3957.000000# NAs 0.000000# Minimum -19.747002# Maximum 13.019382# 1. Quartile -0.809025# 3. Quartile 1.163675# Mean 0.103536# Median 0.100812# Sum 409.692518# SE Mean 0.032307# LCL Mean 0.040196# UCL Mean 0.166876# Variance 4.130064# Stdev 2.032256# Skewness -0.410358# Kurtosis 6.600148可以看到,苹果公司股票的对数收益率存在左偏厚尾现象。
绘制对数收益率的直方图:
# 绘制对数收益率的直方图hist(x,nclass = 30,xlab = " ",ylab=" ",main = "Apple Log Returns")
图13
作核密度估计图并叠加正态密度估计:
# 作核密度估计图并叠加正态密度估计density_x<-density(x)axis_x<-seq(min(x),max(x),length.out=100)density_norm<-dnorm(axis_x,mean(x),sd(x))plot(density_x,xlab = " ",main = "Apple Log Return")lines(axis_x,density_norm,col="red")legend("topleft", lty=1,col=c("black", "red"), legend=c("Kernel density est.", "Parametric normal density est."),bty = "n")
图14
可以看到,苹果股票的对数收益率的密度比正态密度明显厚尾,并且左尾比右尾长。
均值为零的检验:
# 均值为0的检验t.test(x)$p.value# [1] 0.001362457单独计算偏度并检验其是否显著异于0:
# 单独计算偏度并检验其是否显著异于0skew_x<-basicStats(x)["Skewness",1]skew_x/sqrt(6/length(x))# [1] -10.53829标准化值的绝对值超过1.96,在0.05水平下拒绝偏度等于零的假设。
单独计算峰度并检验其是否显著异于0:
# 单独计算峰度并检验其是否显著异于0 kurt_x<-basicStats(x)["Kurtosis",1]kurt_x/sqrt(6/length(x))# [1] 169.4966标准化值的绝对值超过1.96,在0.05水平下拒绝峰度等于零的假设。
正态性JB检验:
# 正态性JB检验x<-as.vector(x)normalTest(x,method = "jb")# Asymptotic p Value: < 2.2e-16在0.05水平下拒绝对数收益率服从正态分布的假设。
参考文献:《金融时间序列分析分析讲义》. 李东风. 北京大学. 2022年
https://mp.weixin.qq.com/s?__biz=MzkzOTQwMTM5MA==&mid=2247483879&idx=1&sn=4b7a5fead88c48040d6e81aa881acd41&chksm=c2f0c826f5874130dd0f2c9666b4ddd4b22292e0cc32a8db2a575964884d7b677f32e255ebdc&cur_album_id=2557243622212141057&scene=189#wechat_redirect
金融数据及其特征(3)目录大纲
金融数据的图形时间序列曲线图K线图密度估计QQ图散点图与回归直线正文部分
1. 金融数据的图形1.1 时间序列曲线图苹果公司2021年日收盘价的时间序列图:
# 时间序列曲线图# 苹果公司2021年日收盘价的时间序列图chartSeries(AAPL,type = "l",subset = "2021",TA=NULL,name = "Apple Stock Price", theme = chartTheme("white"),major.ticks = "months",minor.ticks = FALSE)
图1
用ggplot2包的作图功能则可以进行较多的控制,比如对时间坐标轴的精细控制。如:
library(ggplot2)library(tibble)# tibble建立类似data frame的数据框# mapping将time映射到x轴,将price映射到y轴p <- ggplot(data = tibble(time=index(AAPL),price=coredata(AAPL)[,"AAPL.Close"]), mapping = aes(x=time, y=price))# geom_line()线图p + geom_line()
图2
修改时间轴,每5年标数值/每20个月标数值:
# 时间坐标轴以5年为间隔p + geom_line() + scale_x_date(name = "year",date_breaks = "5 years",date_labels = "%Y", date_minor_breaks = "1 year")# 时间坐标轴以20个月为间隔p + geom_line() + scale_x_date(date_breaks = "20 months",date_labels = "%Y-%m")
图3
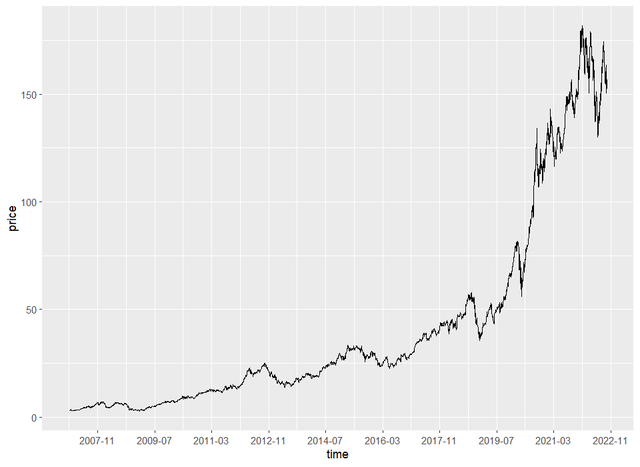
图4
也可以人为制定坐标轴数值:
# 人为制定坐标轴数值library(lubridate)x_date<-make_date(c(2008,2012,2019))p+geom_line()+ scale_x_date(name="year",breaks = x_date,date_labels = "%Y", date_minor_breaks = "1 year")x_date<-as.Date(c("2008-05-30","2019-06-20"))p+geom_line()+ scale_x_date(breaks = x_date,date_labels = "%Y-%m-%d")
图5

图6
可以要求日期旋转45度显示:
# 要求日期旋转45度显示p+geom_line()+ scale_x_date(name = "year",date_labels = "%y-%m-%d")+ theme(axis.text.x = element_text(angle = 45,vjust = 1,hjust = 1))
图7
1.2 K线图苹果公司2021年日收盘价的K线图,带有成交量:
# K线图# 苹果公司2021年日收盘价的K线图,带有成交量chartSeries(AAPL,subset = "2021",theme = chartTheme("white"), name = "Apple Stock Price",major.ticks = "months",minor.ticks = FALSE)
图8
不带有成交量:
# 不带有成交量chartSeries(AAPL,subset = "2021",TA=NULL,theme = chartTheme("white"), name = "Apple Stock Price",major.ticks = "months",minor.ticks = FALSE)
图9
仅画一个月:
# 仅画一个月chartSeries(AAPL,subset = "2021-12",theme = chartTheme("white"), name = "Apple Stock Price",major.ticks = "auto",minor.ticks = FALSE)
图10
1.3 密度估计苹果公司2021年对数收益率的直方图:
# 密度估计# 苹果公司2021年对数收益率的直方图x<-logret.AAPL["2021"]hist(x,xlab = " ",ylab=" ",main = "Apple 2021 Log Returns")
图11
作核密度估计图并叠加正态密度估计:
# 作核密度估计图并叠加正态密度估计density_x<-density(x)axis_x<-seq(min(x),max(x),length.out=100)density_norm<-dnorm(axis_x,mean(x),sd(x))plot(density_x,xlab = " ",main = "Apple Log Return")lines(axis_x,density_norm,col="red")legend("topleft", lty=1,col=c("black", "red"), legend=c("Kernel density est.", "Parametric normal density est."),bty = "n")
图12
1.4 QQ图苹果公司2021年对数收益率的QQ图:
# QQ图qqnorm(x,main = "Apple 2021 Log Return")qqline(x,col="red")
图13
可以看到,苹果公司2021年对数收益率的分布十分接近正态分布。
1.5 散点图与回归直线读入IBM和S&P的月度收益率数据,从1926-01到2011-09, 并转换为xts格式,时间下标改为yearmon格式:
library(tidyverse) # Wickham的数据整理的整套工具library(lubridate) # 日期和日期时间数据处理library(quantmod) # 金融数据的整理与作图功能# 散点图与回归直线# 读取IBM和S&P的月度收益率data<-read_table("ibmsp.txt", col_types = cols(.default=col_double(),date=col_date(format = "%Y%m%d")))# 转换成时间序列数据ibmsp<-xts(data[,2:3],order.by = data$date)# 时间格式改为年月格式tclass(ibmsp)<-"yearmon"head(ibmsp)# ibm sp# 1月 1926 -0.010381 0.022472# 2月 1926 -0.024476 -0.043956# 3月 1926 -0.115591 -0.059113# 4月 1926 0.089783 0.022688# 5月 1926 0.036932 0.007679# 6月 1926 0.068493 0.043184IBM收益率的时间序列图:
# IBM收益率的时间序列图chartSeries(ibmsp[,"ibm"],type = "l",TA=NULL,name = "IBM Monthly Returns", theme = chartTheme("white"),major.ticks = "years",minor.ticks = FALSE)
图14
S&P收益率的时间序列图:
# S&P收益率的时间序列图chartSeries(ibmsp[,"sp"],type = "l",TA=NULL,name = "S&P Monthly Returns", theme = chartTheme("white"),major.ticks = "years",minor.ticks = FALSE)
图15
IBM收益率对标准普尔指数收益率的散点图:
# IBM收益率对标准普尔指数收益率的散点图x<-coredata(ibmsp)plot(x[,"sp"],x[,"ibm"],pch=16,cex=0.2,xlab = "S&P",ylab = "IBM")
图16
计算相关系数:
# 计算相关系数cor.test(x[,"sp"],x[,"ibm"])[["estimate"]][["cor"]]# [1] 0.6395979cor.test(x[,"sp"],x[,"ibm"])[["p.value"]]# [1] 1.851282e-119相关系数为0.64,并且显著异于0。
作线性回归并在散点图上叠加回归直线:
# 作线性回归并在散点图上叠加回归直线x<-as.data.frame(coredata(ibmsp))plot(x[,"sp"],x[,"ibm"],pch=16,cex=0.2,xlab = "S&P",ylab = "IBM")lm1<-lm(ibm~sp,data = x)summary(lm1)## Call:# lm(formula = ibm ~ sp, data = x)# # Residuals:# Min 1Q Median 3Q Max # -0.279155 -0.032137 -0.002261 0.030647 0.280313 # # Coefficients:# Estimate Std. Error t value Pr(>|t|) # (Intercept) 0.008974 0.001706 5.259 1.76e-07 ***# sp 0.818776 0.030707 26.664 < 2e-16 ***# ---# Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1# # Residual standard error: 0.05443 on 1027 degrees of freedom# Multiple R-squared: 0.4091, Adjusted R-squared: 0.4085 # F-statistic: 711 on 1 and 1027 DF, p-value: < 2.2e-16abline(lm1,col="red",lwd=2)
图17
回归方程为:
参考文献:《金融时间序列分析分析讲义》. 李东风. 北京大学. 2022年
